Bất phương trình bậc nhất 2 ẩn - lý thuyết và bài tập Toán 10

1. Định nghĩa bất phương trình số 1 2 ẩn

Bất phương trình số 1 2 ẩn x và hắn đem dạng tổng quát tháo như sau:

Bạn đang xem: Bất phương trình bậc nhất 2 ẩn - lý thuyết và bài tập Toán 10

$ax+by\leq c(ax+by<c, ax+by\geq c, ax+by>c)$

Trong đó:

• a, b, c là những số thực mang lại trước

• a và b ko nằm trong vị 0

• x và hắn là những trở thành (ẩn số)

Cặp trở thành số $(x_0;y_0)$ sao mang lại $ax_0+by_0c$ là bất đẳng thức đích thì cặp trở thành số này được gọi là 1 trong nghiệm của bất phương trình $ax+by\leq c$.

Ví dụ về bất phương trình số 1 2 ẩn: $4x+2y>1$; $x-2y<-2$;...

2. Miền nghiệm của bất phương trình số 1 2 ẩn

2.1. Định lý

Miền nghiệm của bất phương trình số 1 2 ẩn được màn trình diễn bên trên mặt mày phẳng lặng toạ chừng Oxy. Trong mặt mày phẳng lặng toạ chừng Oxy, tụ tập những điểm đem toạ chừng đó là nghiệm của bất phương trình số 1 2 ẩn được gọi là miền nghiệm của bất phương trình cơ.

Ví dụ: Miền nghiệm (phần không trở nên gạch) của bất phương trình $3x-2y>-6$ được màn trình diễn theo như hình bên dưới đây:

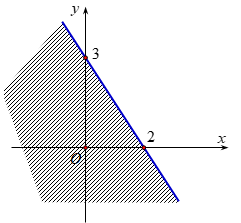
2.2. Biểu thao diễn miền nghiệm của bất phương trình số 1 2 ẩn

Cho mặt mày phẳng lặng toạ chừng Oxy, đem đường thẳng liền mạch d: $ax+by+c=0$ phân tách Oxy trở nên 2 nửa mặt mày phẳng lặng, một trong những nhị nửa mặt mày phẳng lặng cơ chứa chấp những điểm đem toạ chừng thoả mãn bất phương trình số 1 2 ẩn $ax+by+c>0$, nửa mặt mày phẳng lặng còn sót lại chứa chấp những điểm đem toạ chừng thoả mãn bất phương trình số 1 2 ẩn $ax+by+c<0$.

Để xác lập và màn trình diễn miền nghiệm của bất phương trình $ax+b+c<0$, những em học viên triển khai theo gót quá trình sau đây:

• Bước 1: Vẽ đường thẳng liền mạch $d:ax+by+c=0$

• Bước 2: Xét điểm $M(x_0;y_0)$ ko nằm trong đường thẳng liền mạch d. Thường ở đoạn này, tao tiếp tục lấy điểm M là gốc toạ chừng.

• Bước 3: Tính $ax_0+by_0$ và đối chiếu độ quý hiếm với c.

• Bước 4: Kết luận

  • Nếu $ax_0+by_0<c$ thì nửa mặt mày phẳng lặng chứa chấp điểm $M_0$ là miền nghiệm của bất phương trình ax+byc

  • Nếu $ax_0+by_0>c$ thì nửa mặt mày phẳng lặng bờ d ko chứa chấp điểm $M_0$ đó là miền nghiệm của bất phương trình ax+byc

Lưu ý: Miền nghiệm của bất phương trình 2 ẩn ax_0+by_0<c đó là miền nghiệm của bất phương trình 2 ẩn $ax_0+by_0\leq c$ loại bỏ đường thẳng liền mạch $ax+by=0$.

Xét ví dụ tại đây nhằm hiểu rộng lớn về kiểu cách màn trình diễn miền nghiệm của bất phương trình số 1 2 ẩn lớp 10:

Ví dụ 1: Biểu thao diễn miền nghiệm của bất phương trình 2 ẩn $2x-y\geq 0$

Hướng dẫn giải:

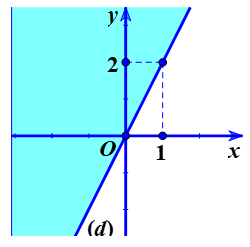
Trong mặt mày phẳng lặng toạ chừng Oxy, vẽ đường thẳng liền mạch $(d):2x-y=0$. Ta được đường thẳng liền mạch (d) phân tách mặt mày phẳng lặng Oxy trở nên 2 nửa. Chọn điểm $M(1;0)$ ko nằm trong đường thẳng liền mạch (d), tao thấy M là nghiệm của bất phương trình số 1 2 ẩn tiếp tục mang lại.

Vì vậy, miền nghiệm cần thiết lần đó là nửa mặt mày phẳng lặng bờ (d) và chứa chấp điểm $M(1;0)$ (miền ko được tô màu xanh lá cây ở hình vẽ).

Ví dụ 2: Biểu thao diễn miền nghiệm của bất phương trình số 1 2 ẩn: $-x+2+2(y-2)<2(1-x)$

Hướng dẫn giải:

$\Leftrightarrow -x+2+2(y-2)<2(1-x)$

$\Leftrightarrow -x+2+2y-4<2-2x$

$\Leftrightarrow x+2y<4 (1)$

Biểu thao diễn miền nghiệm bên trên mặt mày phẳng lặng Oxy:

• Vẽ đường thẳng liền mạch $x+2y=4$

• Thay toạ chừng (0;0) nhập bất phương trình (1), tao được 0+0<4 => (0;0) là một trong những nghiệm của bất phương trình.

Vậy miền nghiệm của bất phương trình là phần mặt mày phẳng lặng không trở nên gạch men nhập hình vẽ tiếp sau đây.

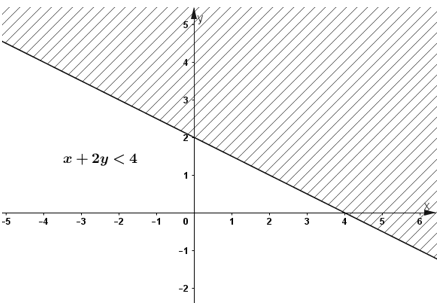
Ví dụ 3: Biểu thao diễn miền nghiệm của bất phương trình số 1 2 ẩn: $3(x-1)+4(y-2)<5x-3$

Hướng dẫn giải:

$\Leftrightarrow 3(x-1)+4(y-2)<5x-3$

$\Leftrightarrow 3x-3+4y-8<5x-3$

$\Leftrightarrow -2x+4y<8$

$\Leftrightarrow x-2y>-4 (2)$

Biểu thao diễn miền nghiệm bên trên mặt mày phẳng lặng Oxy:

• Vẽ đường thẳng liền mạch $x-2y=-4$

• Thay toạ chừng (0;0) nhập bất phương trình (2), tao được: 0+0>-4 (đúng) => (0;0) là 1 trong nghiệm của bất phương trình.

Vậy miền nghiệm của bất phương trình đề bài xích là phần mặt mày phẳng lặng không trở nên gạch men nhập hình vẽ tại đây.

Đăng ký tức thì khóa huấn luyện DUO sẽ được lên quãng thời gian ôn ganh đua chất lượng tốt nghiệp sớm nhất!

3. Hệ bất phương trình số 1 2 ẩn

Hệ bất phương trình số 1 2 ẩn cũng tương tự động như hệ bất phương trình một ẩn tiếp tục học tập ở những bài xích trước. 

Hệ bất phương trình số 1 2 ẩn bao gồm một vài bất phương trình số 1 2 ẩn x và hắn tuy nhiên tao cần thiết lần những nghiệm cộng đồng của bọn chúng. Mỗi nghiệm cộng đồng này được gọi là 1 trong nghiệm của hệ bất phương trình số 1 2 ẩn tiếp tục mang lại.

Cũng tương tự như bất phương trình số 1 2 ẩn, tao hoàn toàn có thể màn trình diễn miền nghiệm của hệ với quá trình triển khai tương tự như xét bất phương trình số 1 2 ẩn. Để hiểu cụ thể rộng lớn cơ hội xét miền nghiệm dạng hệ bất phương trình, tao nằm trong coi ví dụ bên dưới đây:

Ví dụ 1: Biểu thao diễn miền nghiệm của hệ bất phương trình số 1 2 ẩn sau:

Xem thêm: Cách tải Shopee trên máy tính đơn giản cho người mới bắt đầu

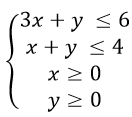
Hướng dẫn giải:

Vẽ những đường thẳng liền mạch sau đây:

$d_1: 3x+y=6$

$d_2: x+y=4$

$d_3: x=0(Oy)$

$d_4: y=0(Ox)$

Do điểm $M_0(1;1)$ đem toạ chừng thoả mãn từng bất phương trình nhập hệ, nên tao tô đậm những nửa mặt mày phẳng lặng bờ $(d_1)$, $(d_2)$, $(d_3)$, $(d_4)$ ko chứa chấp điểm $M_0$. Miền không trở nên tô đậm nhập hình tiếp sau đây đó là miền nghiệm của hệ bất phương trình 2 ẩn đề bài xích.

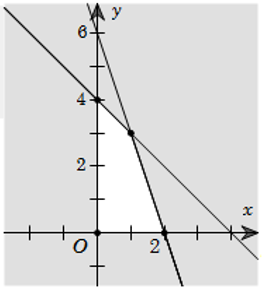
Ví dụ 2: Xác tấp tểnh miền nghiệm của hệ bất phương trình số 1 2 ẩn sau:

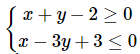
Hướng dẫn giải:

Vẽ đường thẳng liền mạch $(d):x+y-2=0$, $(d’’):x-3y+3=0$ bên trên mặt mày phẳng lặng Oxy.

Xét điểm gốc toạ chừng $O(0;0)$: Điểm O ko nên là nghiệm của bất phương trình $x+y-2\geq 0$ và $x-3y+3/leq 0$.

Như vậy, miền nghiệm của hệ bất phương trình đề bài xích là phần mặt mày phẳng lặng ko được tô color ở hình vẽ tiếp sau đây.

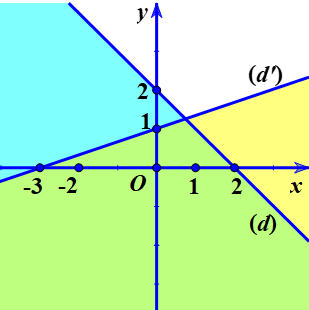
Ví dụ 3: Xác tấp tểnh miền nghiệm của hệ bất phương trình số 1 2 ẩn sau:

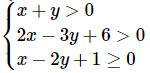
Hướng dẫn giải:

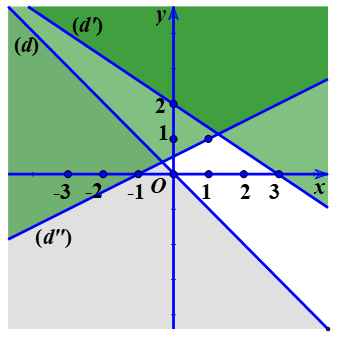
Vẽ những đường thẳng liền mạch sau bên trên mặt mày phẳng lặng toạ chừng Oxy:

$(d):x+y=0$

$(d’):2x-3y+6=0$

$(d’’):x-2y+1=0$

Xét điểm $O(0;0)$: Điểm 0 là nghiệm của bất phương trình $2x-3y+6>0$ và $x-2y+1\geq 0$.

Xét điểm $M(1;0)$: Điểm M là nghiệm của bất phương trình $x+y>0$ => điểm M nằm trong miền nghiệm của bất phương trình $x+y>0$.

Vậy miền nghiệm cần thiết lần là phần mặt mày phẳng lặng ko được tô color nhập hình vẽ tiếp sau đây.

4. kề dụng hệ bất phương trình số 1 2 ẩn nhập Việc kinh tế

Hệ bất phương trình số 1 2 ẩn thông thường được vận dụng thật nhiều nhập những Việc tài chính thực tiễn. Loại Việc này còn có cả một ngành toán học tập nghiên cứu và phân tích mang tên gọi là Quy hoạch tuyến tính.

Cùng xét ví dụ tiếp sau đây nhằm hiểu cơ hội giải Việc tài chính vận dụng hệ bất phương trình số 1 2 ẩn:

Ví dụ: Có 1 xưởng phát hành 2 loại thành phầm, từng cân nặng thành phầm loại I cần thiết 2 cân nặng nguyên vật liệu và 30 giờ phát hành, nút ROI mang đến là 40.000 đồng. Mỗi cân nặng thành phầm loại II cần thiết 4 cân nặng nguyên vật liệu và 15 giờ phát hành, nút ROI mang đến là 30.000 đồng. Xưởng đem 200 cân nặng nguyên vật liệu và 120 giờ thao tác làm việc. Hỏi giám đốc của xưởng nên mang lại phát hành từng loại thành phầm từng nào cân nặng để sở hữu nút ROI cao nhất?

Hướng dẫn giải:

Gọi x $(x_0)$ là số cân nặng tuy nhiên loại I cần thiết phát hành, hắn $(y_0)$ là số cân nặng loại II cần thiết phát hành.

Từ đề bài xích suy ra: số nguyên vật liệu nên dùng là $2x+4y$, thời lừa lọc là $30x+15y$, nút ROI chiếm được là $40000x+30000y$.

Theo fake thiết đề bài xích, xưởng đem 200kg nguyên vật liệu và 120 giờ thao tác làm việc => $2x+4y\leq 200$ hoặc $x+2y-100\leq 0$, $30x+15y\leq 1200$ hoặc $2x+y-80\leq 0$.

Từ cơ, Việc trở thành: Tìm x và hắn thỏa mãn nhu cầu hệ bất phương trình 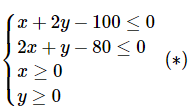sao mang lại $H(x;y)=40000x+30000y$ đạt độ quý hiếm lớn số 1.

Trong mặt mày phẳng lặng Oxy, vẽ những đường thẳng liền mạch $(d’):x+2y-100=0$ và $(d’’):2x+y-80=0$.

Khi cơ miền nghiệm của hệ bất phương trình 2 ẩn (*) là phần mặt mày phẳng lặng ko được tô color ở hình vẽ tiếp sau đây.

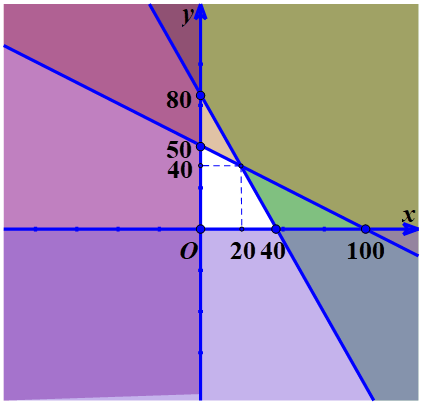
Giá trị lớn số 1 của $H(x;y)=40000x+30000y$ đạt độ quý hiếm bên trên một trong số điểm (0;0), (40;0), (0;50), (20;40).

Ta có: H(0;0)=0, H(40;0)=1600000, H(0;50)=1500000, H(20;40)=2000000

Giá trị lớn số 1 của H(x;y)=2000000 Khi (x;y)=(20;40)

Vì vậy, xưởng cần thiết phát hành 20kg thành phầm loại I và 40kg thành phầm loại II để sở hữu nút ROI lớn số 1.

Bài ghi chép tiếp tục tổ hợp toàn cỗ lý thuyết bất phương trình  số 1 2 ẩn Toán lớp 10, tất nhiên ví dụ đem giải cụ thể minh hoạ để giúp đỡ những em học viên làm rõ rộng lớn những phần kỹ năng VUIHOC mong muốn truyền đạt. Để phát âm và học tập nhiều hơn thế nữa về Toán lớp 10, Toán trung học phổ thông,... những em truy vấn benhhocmatngu.vn hoặc ĐK tức thì bên trên phía trên nhé!