benhhocmatngu
benhhocmatngu
Trang chủ Uncategorized 12 Công Thức Tính Thể Tích Khối Chóp Kèm Ví Dụ Cụ Thể

12 Công Thức Tính Thể Tích Khối Chóp Kèm Ví Dụ Cụ Thể

Tổng hợp ý toàn cỗ lý thuyết cơ phiên bản và 12 công thức tính thể tích khối chóp, ví dụ ví dụ, cùng theo với cách thức giải bài xích luyện nhanh gọn. Các em học viên lớp 12 ko thể bỏ lỡ.

Trong lịch trình hình học tập trung học phổ thông, những bài xích luyện về thể tích khối chóp luôn luôn xuất hiện tại vô đề thi đua ĐH. Vì vậy, học viên cần thiết cầm dĩ nhiên những kiến thức và kỹ năng cơ phiên bản về khối chóp và nằm trong ở lòng công thức tính thể tích khối chóp. Cùng VUIHOC ôn luyện lý thuyết và điểm lại 12 công thức tính thể tích khối chóp hay được dùng nhé! 

Bạn đang xem: 12 Công Thức Tính Thể Tích Khối Chóp Kèm Ví Dụ Cụ Thể

1. Ôn luyện lý thuyết thể tích khối chóp lớp 12

Thể tích của một vật là lượng không khí nhưng mà vật ấy cướp. Thể tích thông thường với đơn vị chức năng đo là lập phương của khoảng cách. 

Thể tích khối chóp

Trong lịch trình học tập, thể tích khối chóp được xem theo đòi công thức:

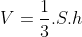
V= \frac{1}{3}.S.h

Trong đó: 

  • S là diện tích S đáy
  • h là chiều cao

Ngoài rời khỏi, nhằm đáp ứng cho những bài xích thói quen tỉ số thể tích nhị khối chóp tam giác thông thường xuất hiện tại trong những việc ôn luyện thể tích khối chóp lớp 12, tao đạt thêm công thức:

Nếu A’, B’, C’ là tía điểm theo thứ tự phía trên những cạnh SA, SB, SC của hình chóp tam giác S.ABC thì Lúc đó:

Công thức tỉ lệ thành phần thể tích khối chóp tam giác

2. Các công thức tính thể tích khối chóp dễ dàng nắm bắt nhất

Nhìn công cộng, với thật nhiều những cách thức và công thức dùng làm tính được thể tích khối chóp, đôi khi vận dụng thể tích khối chóp nâng lên. Tuy nhiên, vô bài xích ôn tập này, VUIHOC chỉ tổ hợp 12 công thức tính thể tích khối chóp thông thường bắt gặp và dễ dàng dùng nhất nhằm giải những việc hình học tập với tương quan cho tới thể tích khối chóp. 

2.1. Cách tính thể tích khối chóp xuất hiện mặt mày vuông góc đáy

Để phát hiện những việc thể tích hình chóp vận dụng công thức này, tao xét Điểm sáng của hình chóp nhưng mà đề bài xích cho tới. Nếu hình chóp với nhị mặt mày mặt nằm trong vuông góc với lòng và độ cao của khối chóp đó là phó tuyến của nhị mặt mày cơ, tao vận dụng cách thức này.

Để xác lập lối cao của hình chóp, tao áp dụng quyết định lý sau đây:

Phương pháp tính thể tích khối chóp - Toán lớp 12

Ta nằm trong xét ví dụ minh họa tại đây nhằm hiểu rộng lớn về phong thái tính thể tích khối chóp này.

Ví dụ: Cho hình chóp S.ABC với lòng ABC là tam giác vuông bên trên B, BA = 3a, BC = 4a; mặt mày bằng (SBC) vuông góc với mặt mày bằng (ABC). hiểu SB=2a√3 và ∠(SBC)=30º, tính thể tích khối chóp S.ABC.

Bài luyện ví dụ tính thể tích khối chóp

Hướng dẫn giải

Ta kẻ SH vuông góc với đoạn thằng BC (với H phía trên BC)

Từ cơ tao có:

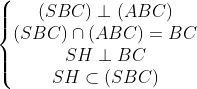
\left\{\begin{matrix} (SBC) \perp (ABC)\\ (SBC) \cap (ABC) = BC\\ SH \perp BC\\ SH\subset (SBC) \end{matrix}\right.

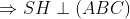
\Rightarrow SH \perp (ABC)

Ta xét tam giác SHB vuông bên trên H, tao có:

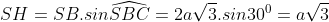
SH = SB.sin\widehat{SBC} = 2a\sqrt{3}.sin30^{0} = a\sqrt{3}

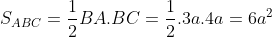
S_{ABC} = \frac{1}{2}BA.BC = \frac{1}{2}.3a.4a = 6a^{2}

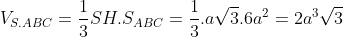
V_{S.ABC} = \frac{1}{3}SH.S_{ABC} = \frac{1}{3}.a\sqrt{3}.6a^{2} = 2a^{3}\sqrt{3}

>>>Nắm trọn vẹn cỗ kiến thức và kỹ năng hình học tập không khí ôn thi đua đảm bảo chất lượng nghiệp trung học phổ thông ngay<<<

2.2. Phương pháp tính thể tích khối chóp với cạnh mặt mày vuông góc đáy

Phương pháp giải:

Ta với công thức thể tích khối chóp là 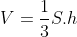V = \frac{1}{3}S.h với S là diện tích S lòng, h là độ cao. Khối chóp với cạnh mặt mày vuông góc với lòng suy rời khỏi cạnh mặt mày vuông góc với lòng là lối cao của chóp hoặc h=độ lâu năm cạnh mặt mày vuông góc với lòng.

Ví dụ minh họa: Cho khối chóp S.ABC với SA vuông góc với lòng, SA= 4; AB= 6; BC= 10 và CA= 8. Tính thể tích khối chóp S.ABC.

A. V= 40

B. V= 96

C. V= 32

D. V= 64

Giải:

Ví dụ minh họa bài xích thói quen thể tích khối chóp 

2.3. Thể tích khối chóp S.ABCD với lòng là hình vuông

Đối với một khối chóp abcd với lòng là hình vuông vắn, tao với ví dụ minh họa sau đây:

Ví dụ: Cho khối chóp S.ABCD với lòng là hình vuông vắn cạnh a, SA vuông góc với đấy và SC tạo ra với mp (SAB) một góc 30 chừng. Tính thể tích khối chóp?

Giải:

Ta với tự ABCD là hình vuông vắn nên có 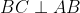BC \perp AB

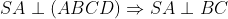
SA \perp (ABCD) \Rightarrow SA \perp BC

Từ 2 điều bên trên tao hoàn toàn có thể suy rời khỏi được 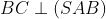BC \perp (SAB)

Do cơ tao có 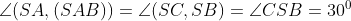\angle (SA, (SAB)) = \angle (SC,SB) = \angle CSB = 30^{0}

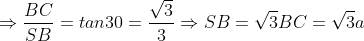
\Rightarrow \frac{BC}{SB} = tan30 = \frac{\sqrt{3}}{3} \Rightarrow SB = \sqrt{3}BC = \sqrt{3}a

Theo quyết định lý Pitago:

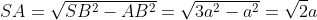
SA = \sqrt{SB^{2} - AB^{2}} = \sqrt{3a^{2} - a^{2}} = \sqrt{2}a

Do vậy:

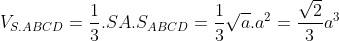
V_{S.ABCD} = \frac{1}{3}.SA.S_{ABCD} = \frac{1}{3}\sqrt{a}.a^{2} = \frac{\sqrt{2}}{3}a^{3}

2.4. Tìm thể tích khối chóp lập phương

Đây là dạng khối chóp đặc biệt quan trọng vì thế những mặt mày của khối chóp đều là hình vuông vắn (lập phương). Vì vậy, cách thức tính thể tích khối chóp lập phương cực kỳ đơn giản: 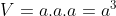V=a.a.a=a^{3} (do những cạnh của hình lập phương đều phải sở hữu chừng lâu năm đều bằng nhau, một cách tiếp theo của công thức thể tích là s3, vô cơ s là chừng lâu năm cạnh của hình lập phương)

Ví dụ minh họa:

Tính thể tích khối lập phương có tính lâu năm lối chéo cánh là 27 centimet.

Giải:

Độ lâu năm cạnh của khối lập phương là: 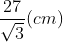\frac{27}{\sqrt{3}} (cm)

Vậy thể tích của khối lập phương cần thiết thám thính là: 

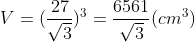
V = (\frac{27}{\sqrt{3}})^{3} = \frac{6561}{\sqrt{3}} (cm^{3})

2.5. Thể tích khối chóp lăng trụ tam giác đều

Nếu một hình học tập xuất hiện mặt mày là hình bình hành, nhị mặt mày lòng tuy vậy song và đều bằng nhau thì nhiều giác này là hình lăng trụ. Một hình lăng trụ xuất hiện lòng là một trong tam giác đều thì này là hình lăng trụ tam giác đều.

Ta nằm trong xét ví dụ sau nhằm tính thể tích khối chóp lăng trụ tam giác đều:

Xem thêm: Lý Thuyết Dấu Của Tam Thức Bậc Hai Và Các Bài Tập Vận Dụng

Ví dụ: Cho hình lăng trụ ABC.A’B’C’ với lòng ABC là tam giác đều cạnh bởi vì a = 2 centimet và độ cao là h = 3 centimet. Hãy tính thể tích hình lăng trụ này. 

Giải:

Bài thói quen thể tích khối chóp lăng trụ

Vì lòng là tam giác đều cạnh a nên diện tích 

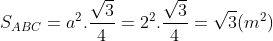
S_{ABC}=a^{2}.\frac{\sqrt{3}}{4}=2^{2}.\frac{\sqrt{3}}{4}=\sqrt{3}(m^{2})

Khi này, thể tích là 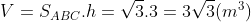V=S_{ABC}.h=\sqrt{3}.3=3 \sqrt{3}(m^{3})

>> Xem thêm: Công thức tính thể tích khối lăng trụ đứng tam giác đều

Nhận tức thì trọn vẹn cỗ kiến thức và kỹ năng và cách thức giải từng dạng bài xích luyện hình học tập không khí với cỗ bí mật độc quyền của VUIHOC

2.6. Cách thám thính thể tích khối chóp lục giác đều

Cùng VUIHOC xét ví dụ minh họa tại đây về thể tích khối chóp lục giác đều.

Ví dụ: Một khối chóp lục giác đều, góc thân thích cạnh mặt mày và mặt mày lòng là 30 chừng, cạnh lòng a. Tính thể tích V của khối chóp? 

Giải:

Đặt S.ABCDEF là hình chóp lục giác đều lòng ABCDEF là hình chóp thỏa mãn nhu cầu đề bài xích tiếp tục rời khỏi. Ta có:

Gọi điểm O là tâm của ABCDEF

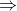\Rightarrow OA = OB = OC = OD = OE = OF = AB = BC = CD = DE = EF = FA = a

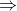
\Rightarrow \DeltaOAB là tam giác đều phải sở hữu cạnh là a

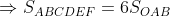
\Rightarrow S_{ABCDEF} = 6S_{OAB}

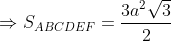
\Rightarrow S_{ABCDEF} = \frac{3a^{2}\sqrt{3}}{2}

Ta có:

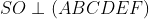
SO \perp (ABCDEF)

\Rightarrow (SA; (\widehat{ABC}DEF)) = \widehat{SAO} = 30^{0}

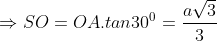
\Rightarrow SO = OA.tan30^{0} = \frac{a\sqrt{3}}{3}

Từ cơ tao được:

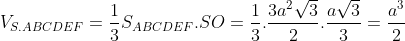
V_{S.ABCDEF} = \frac{1}{3}S_{ABCDEF}.SO = \frac{1}{3}.\frac{3a^{2}\sqrt{3}}{2}.\frac{a\sqrt{3}}{3} = \frac{a^{3}}{2}

2.7. Công thức tính thể tích khối chóp lăng trụ

Công thức tính thể tích lăng trụ: Khối lăng trụ với diện tích S lòng B và độ cao h hoàn toàn có thể tích được xem theo đòi công thức: V=B.h

Công thức tính thể tích khối chóp lăng trụ

2.8. Tính thể tích khối chóp lúc biết 3 cạnh bên

Đây là dạng đặc biệt quan trọng trong những việc tính thể tích khối chóp. Khi bắt gặp tình huống này, những em dùng công thức tổng quát lác sau: 

Ta với BC=a, CA=b, AB=c, AD=d, BD=e, CD=f nằm trong khối tứ diện ABCD, công thức tính thể tích của tứ diện 6 cạnh như sau:

V=12M+N+P+Q, vô đó:

Công thức tính thể tích khối chóp tứ diện 6 cạnh

Ví dụ minh họa: Cho khối tứ diện ABCD với AB=CD=8, AD=BC=5 và AC=BD=7. Thể tích khối tứ diện tiếp tục cho tới bởi vì bao nhiêu?

Bài luyện ví dụ minh họa thể tích khối chóp

2.9. Tìm thể tích khối chóp những cạnh song một vuông góc

Ta xét ví dụ minh họa tại đây nhằm hiểu rộng lớn phương pháp tính thể tích khối chóp vô tình huống khối chóp với những cạnh song một vuông góc như sau:

Cho tứ diện SABC với những cạnh SA,SB,SC song một vuông góc cùng nhau. hiểu SA=3a, SB=4a, SC=5a. Tính theo đòi a thể tích V của khối tứ diện SABC.

Giải:

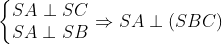
\left\{\begin{matrix} SA \perp SC\\ SA \perp SB \end{matrix}\right. \Rightarrow SA \perp (SBC)

\Rightarrow V_{S.ABC} = \frac{1}{3}SA.S_{SBC} = \frac{1}{6}SA.SB.SC = \frac{1}{6}.3a.4a.5a = 10a^{3}

2.10. Thể tích khối chóp tròn trĩnh xoay

Ta hoàn toàn có thể hay thấy, thể tích khối chóp tròn trĩnh xoay tương tự động như công thức tính thể tích khối chóp:

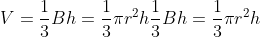
V=\frac{1}{3}Bh=\frac{1}{3}\pi r^{2}h\frac{1}{3}Bh=\frac{1}{3}\pi r^{2}h

Trong công thức bên trên B là diện tích S lòng hình nón, r là nửa đường kính lòng hình nón, h là độ cao của hình nón.

Cùng VUIHOC xét ví dụ minh họa tại đây tính thể tích khối chóp tròn trĩnh xoay:

Bài luyện ví dụ minh họa thể tích khối chóp​​​​​​

Ví dụ bài xích thói quen thể tích khối chóp

>> Xem thêm: Công thức tính thể tích khối tròn trĩnh xoay đúng chuẩn nhất

2.11. Tính thể tích của khối chóp tam giác đều

Đây là dạng toán đặc biệt quan trọng, thông thường xuất hiện tại trong những thắc mắc thám thính điểm 8+. Các em nằm trong xét ví dụ minh họa tại đây nhằm hiểu cơ hội giải dạng bài xích tính thể tích khối chóp này:

Tính thể tích V của khối chóp tam giác đều SABC biết độ cao hình chóp bởi vì h, góc SBA=a

Giải:

Ví dụ bài xích thói quen thể tích khối chóp tam giác đều

2.12. Công thức tính thể tích khối chóp tứ giác đều cạnh lòng bởi vì a

Cùng VUIHOC giải bài xích thói quen thể tích khối chóp tứ giác đều cạnh lòng bởi vì a với bài xích luyện minh họa sau:

Tính thể tích khối chóp tứ giác đều V với toàn bộ những cạnh bởi vì a.

Giải:

Ví dụ bài xích thói quen thể tích khối chóp đều phải sở hữu cạnh lòng bởi vì a

Để ôn luyện kỹ và thành thục rộng lớn 12 công thức tính thể tích khối chóp hao hao áp dụng tính thể tích khối chóp nâng lên, VUIHOC tặng miễn phí những em học viên tệp tin tổ hợp bài xích luyện rèn luyện tinh lọc. Các em lưu giữ lưu về làm tư liệu ôn thi đua nhé!

VUIHOC tiếp tục với những em học viên ôn luyện lại lý thuyết công cộng về thể tích khối chóp và 12 công thức thông thường bắt gặp nhất trong những đề thi đua. Hy vọng rằng sau nội dung bài viết này, những em sẽ không còn bắt gặp nhiều trở ngại vô quy trình ôn luyện và giải toán thể tích khối chóp. Để học tập được rất nhiều những kiến thức và kỹ năng hoặc và cơ hội liệu pháp giải thú vị ôn luyện thi đua trung học phổ thông, truy vấn tức thì benhhocmatngu.vn và ĐK khóa huấn luyện ôn thi đua Nhanh trung học phổ thông thích hợp cho tới cử tử 2004 nhé!

Xem thêm: Bức tranh BlackPink chibi đẹp đến tuyệt vời

Đăng ký tức thì sẽ được những thầy cô tổ hợp kiến thức và kỹ năng và kiến tạo suốt thời gian ôn thi đua trung học phổ thông đạt 9+ sớm tức thì kể từ bây giờ

>> Xem thêm:

  • Tổng hợp ý công thức toán hình 12 không hề thiếu dễ dàng lưu giữ nhất
  • Cách học tập hình học tập không khí đảm bảo chất lượng - toán 12
  • Công thức tính thể tích khối cầu nhanh chóng và đúng chuẩn nhất

BÀI VIẾT NỔI BẬT

7 tips book vé máy bay giá rẻ

Dịp cuối năm cận kề hứa hẹn một mùa du lịch đầy háo hức và sôi động lại tới. Tuy nhiên đây cũng là thời điểm nhiều du khách cùng có kế hoạch vi vu nên chắc chắn giá vé sẽ tăng. Vậy làm thế nào để có thể mua được vé máy bay với chi phí tiết kiệm nhất nhỉ? Bạn hãy cùng ABAY tham khảo một số tips hữu ích dưới đây nhé.