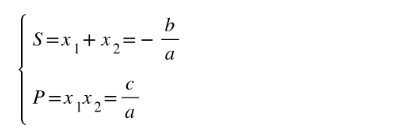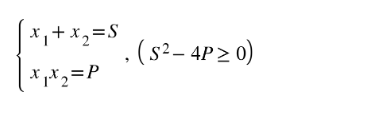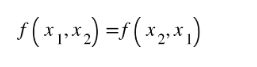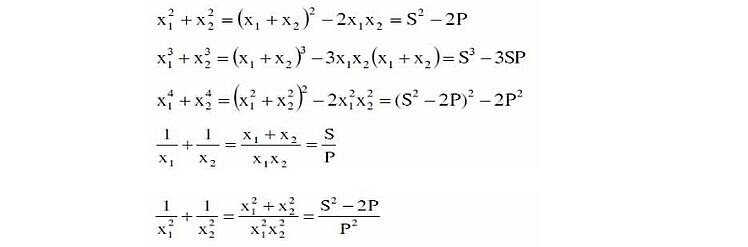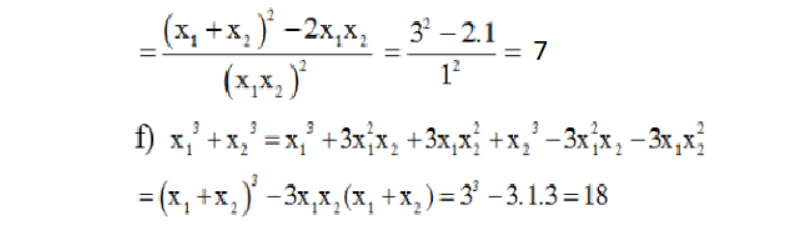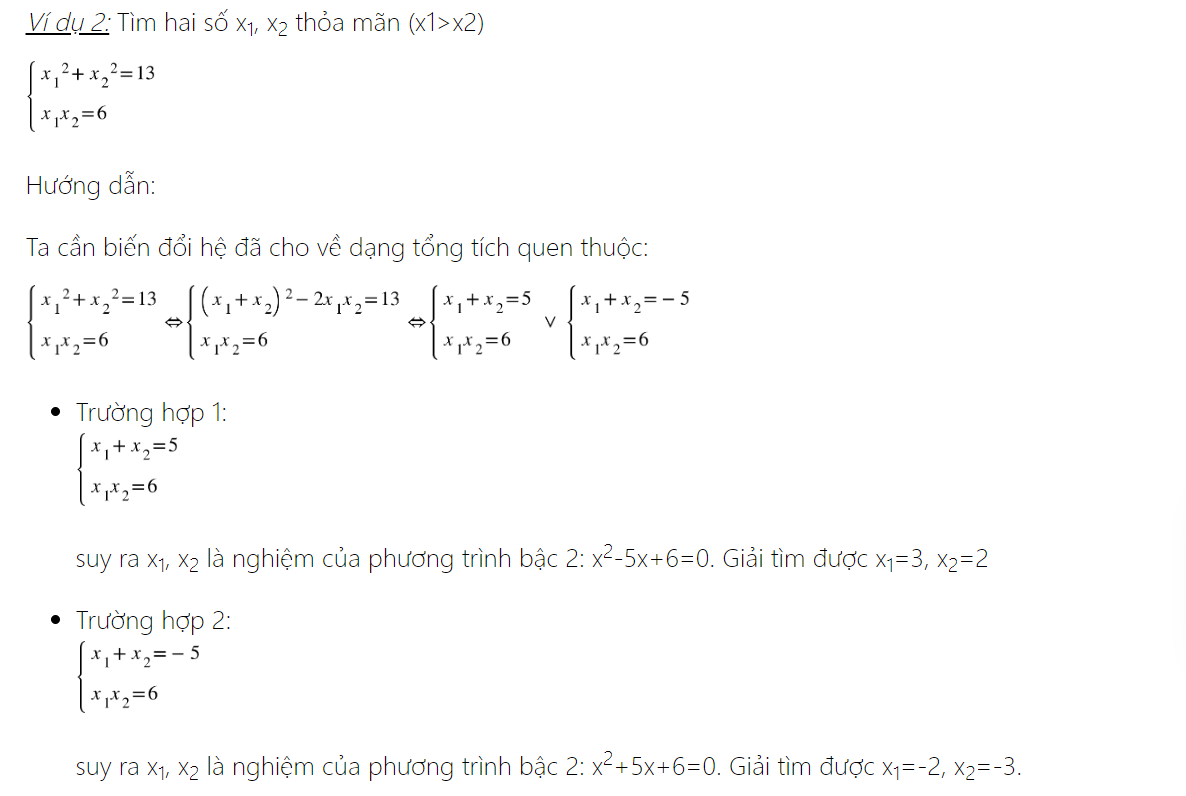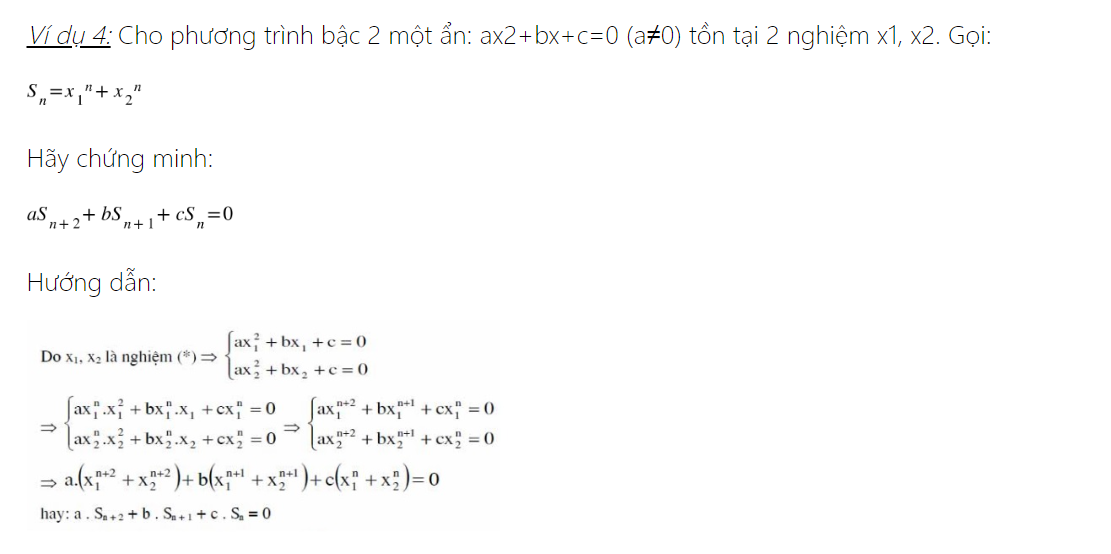Định lý Viet là một trong những trong mỗi kiến thức và kỹ năng cơ bạn dạng tuy nhiên cũng vô nằm trong cần thiết của công tác toán Trung học tập hạ tầng thưa công cộng và vô công tác Toán 9. Đây cũng chính là mục chính thông thường xuyên được phần mềm trong số bài xích luyện trong số kì đua học viên đảm bảo chất lượng, ôn đua tuyển chọn sinh lớp 10 môn Toán. Chính chính vì vậy, nội dung bài viết này HOCMAI tiếp tục share toàn cỗ kiến thức và kỹ năng cơ bạn dạng nên nhớ và những dạng bài xích luyện về quyết định lý Viet nhằm những em học viên hoàn toàn có thể tham lam khảo!
Bạn đang xem: Hệ thức Vi-et và ứng dụng của hệ thức trong giả bài tập HOCMAI
A. Lý thuyết về quyết định lý Viet
1. Định nghĩa
Cho cho 1 phương trình bậc 2 một ẩn đem dạng:
ax² + bx + c = 0 (điều kiện: a≠0)
Khi phương trình bên trên đem 2 nghiệm x1 và x2 thì 2 nghiệm của phương trình này thỏa mãn nhu cầu hệ thức sau:
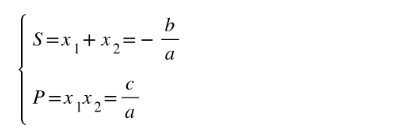
2. Hệ ngược của quyết định lý Viet:
Dựa vô hệ thức Viet tao có: Với một phương trình bậc 2 một ẩn đem nghiệm, tao trọn vẹn hoàn toàn có thể nhẩm nhanh chóng thẳng nghiệm của phương trình bậc 2 một ẩn tiếp tục cho tới vô một vài tình huống sau:
- Nếu a+b+c=0 thì phương trình ax² + bx + c có một nghiệm x1 = 1 và x2 = c/a
- Nếu a-b+c=0 thì phương trình ax² + bx + c đem 2 nghiệm x1 = -1 và x2 = -c/a
3. Định lý hòn đảo của quyết định lý Viet
Giả sử nhì số thực x1 và x2 xác lập thỏa mãn nhu cầu hệ thức sau:
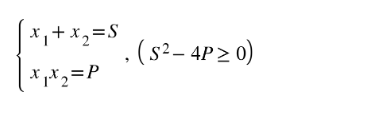
Thì 2 số thực x1 và x2 tiếp tục nghĩ rằng 2 nghiệm của phương trình bậc 2 một ẩn đem dạng:
x2 – Sx + P.. = 0
B. Các dạng bài xích luyện phần mềm quyết định lý Viet
Dạng bài xích luyện 1: Vận dụng hệ thức Viet đề nhì số lúc biết được tổng và tích.
Hướng dẫn giải
Nếu đem 2 số u và v xác lập thỏa mãn nhu cầu điều kiện

thì 2 số u, v được xem là nghiệm của phương trình bậc 2 một ẩn đem dạng: x² – Sx + P.. = 0.
Xem thêm: Bệnh viện 103 có tốt không? • Hello Bacsi
Như vậy, trải qua việc xác lập nhì số u, v , những em học viên tiếp tục trở lại dạng vấn đề giải phương trình bậc 2 mang 1 ẩn:
- Nếu S2 – 4P ≥ 0 thì tồn bên trên u và v.
- Nếu S2 – 4P < 0 sẽ không còn tồn bên trên 2 số thỏa mãn nhu cầu yêu thương cầu
Dạng bài xích luyện 2: gí dụng quyết định ý Viet nhằm tính độ quý hiếm của biểu thức đối xứng
Hướng dẫn giải:
Các phân biệt biểu thức đối xứng: Một biểu thức là biểu thức đối xứng với 2 độ quý hiếm x1, x2 khi tao thay đổi địa điểm x1, x2 lẫn nhau thì độ quý hiếm biểu thức ko thay cho đổi:
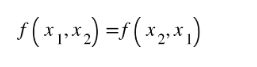
Nếu f là một trong những biểu thức đối xứng thì biểu thức này tiếp tục luôn luôn tồn bên trên những cơ hội màn trình diễn trải qua biểu thức đối xứng đem ẩn là S=x1+x2 và P=x1x2
Một số cơ hội màn trình diễn S và P.. thông thường bắt gặp là:
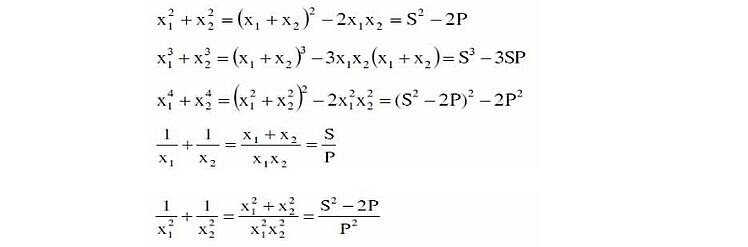
Sau tê liệt, vận dụng quyết định lý Viet, tao đem tao tính giá tốt trị biểu thức cần thiết tìm
Dạng bài xích luyện 3: gí dụng quyết định lý Viet vô những dạng bài xích luyện đem chứa chấp tham lam số
Đối với những bài xích luyện nằm trong dạng phương trình đem chứa chấp thông số, ĐK trước tiên là cần xét những tình huống nhằm phương trình bậc 2 tồn bên trên nghiệm. Sau tê liệt vận dụng quyết định lý Viet tiếp tục thưa phía trên cho tới phương trình, tao sẽ sở hữu được những hệ thức của nhì nghiệm x1, x2 theo đòi thông số tiếp tục cho tới của đề bài xích, tiếp sau đó kết phù hợp với những dữ khiếu nại đề bài xích đề mò mẫm đi ra đáp án.
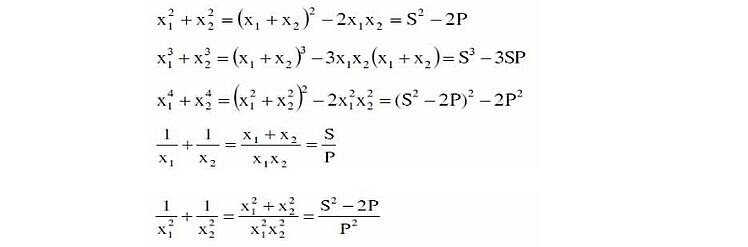


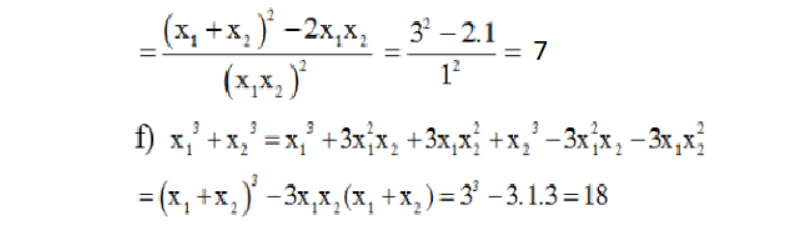

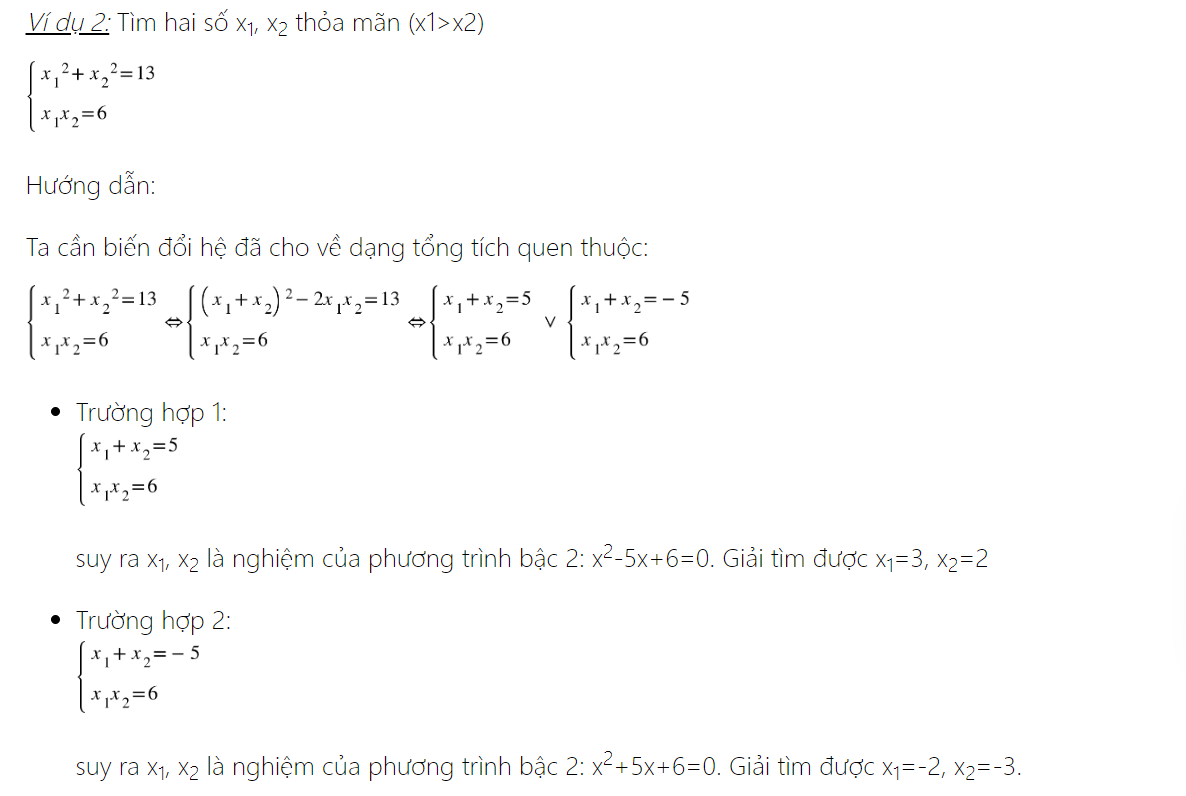


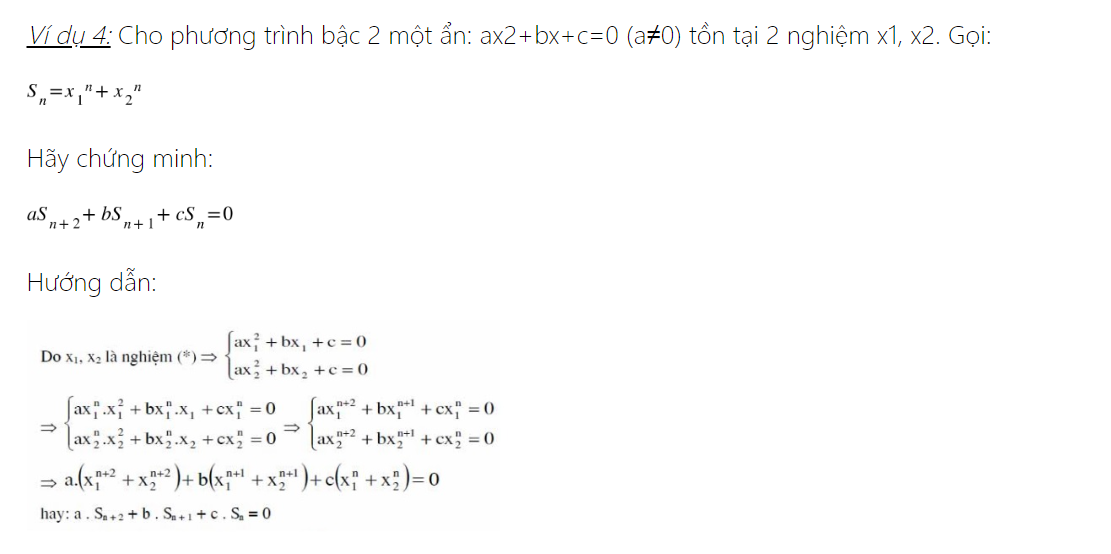




Tham khảo thêm:
Xem thêm: Đặt vé máy bay từ Sài Gòn đi Phú Quốc
Công thức nghiệm phương trình bậc 2
Công thức nghiệm thu sát hoạch gọn