benhhocmatngu
benhhocmatngu
Trang chủ Uncategorized Công thức đường trung tuyến

Công thức đường trung tuyến

GiaiToan.com biên biên soạn và đăng lên tư liệu Công thức chừng lâu năm lối trung tuyến bao hàm những con kiến thức: định nghĩa, đặc điểm lối trung tuyến nhập tam giác vuông, tam giác cân nặng, tam giác đều và công thức tính lối trung tuyến, giúp những em học viên gia tăng, tóm dĩ nhiên kiến thức và kỹ năng cơ phiên bản Toán 10. Chúc chúng ta tiếp thu kiến thức tốt!

A. Đường trung tuyến

- Đường trung tuyến của một đoạn thẳng là một trong những đường thẳng liền mạch trải qua trung điểm của đường thẳng liền mạch bại.

Bạn đang xem: Công thức đường trung tuyến

- Đường trung tuyến nhập tam giác là một trong đoạn trực tiếp nối kể từ đỉnh của tam giác cho tới trung điểm của những cạnh đối lập nó. Mỗi tam giác sở hữu 3 lối trung tuyến.

B. Tính hóa học lối trung tuyến

a. Tính hóa học đường trung tuyến của tam giác

- Ba đường trung tuyến của tam giác đồng quy bên trên một điểm được gọi là trọng tâm.

- Khoảng cơ hội kể từ nhập tâm cho tới từng đỉnh của tam giác bằng \frac{2}{3}đường trung tuyến ứng với đỉnh bại.

- Khoảng cơ hội kể từ nhập tâm cho tới trung điểm từng cạnh vì thế \frac{1}{3} lối trung tuyến ứng với điểm bại.

Ví dụ: Cho tam giác ABC, sở hữu D, E, F theo lần lượt là trung điểm của những cạnh AC, AB, BC.

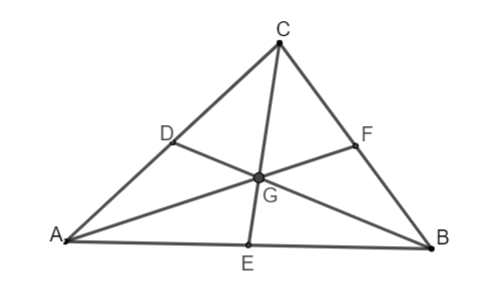Công thức lối trung tuyến

- Gọi G là uỷ thác điểm của những đường thẳng liền mạch BD, AF, CE suy rời khỏi G là trọng tâm tam giác ABC.

Ta sở hữu những đặc điểm sau:

\frac{{CG}}{{CE}} = \frac{{AG}}{{AF}} = \frac{{BG}}{{BD}} = \frac{2}{3}

\frac{{GE}}{{CE}} = \frac{{GF}}{{AF}} = \frac{{GD}}{{BD}} = \frac{1}{3}

b. Tính hóa học lối trung tuyến nhập tam giác vuông

- Đường trung tuyến của tam giác vuông sở hữu những đặc điểm cộng đồng của lối trung tuyến nhập tam giác thông thường. Bên cạnh đó tớ sở hữu những đặc điểm đặc thù sau:

+ Đường trung tuyến nhập tam giác vuông ứng với cạnh huyền vì thế 1/2 cạnh huyền.

Ví dụ: Cho tam giác ABC vuông bên trên C, lối trung tuyến CD

+ Trong một tam giác sở hữu lối trung tuyến ứng với cùng một cạnh nhưng vì 1/2 cạnh bại thì tam giác này là tam giác vuông.

c. Đường trung tuyến nhập tam giác cân

- Trong tam giác cân nặng, tam giác đều, lối trung tuyến ứng với cạnh lòng thì vuông góc với cạnh bại và phân chia tam giác trở nên nhì tam giác đều nhau.

C. Công thức tính lối trung tuyến

- Cho tam giác ABC có tính lâu năm những cạnh AB = c; AC = b; BC = a, những lối trung tuyến {m_a};{m_b};{m_c}

Ví dụ 1: Tam giác ABC sở hữu AB = AC = 10cm, BC = 12cm. Tính chừng lâu năm lối trung tuyến AM.

Hướng dẫn giải

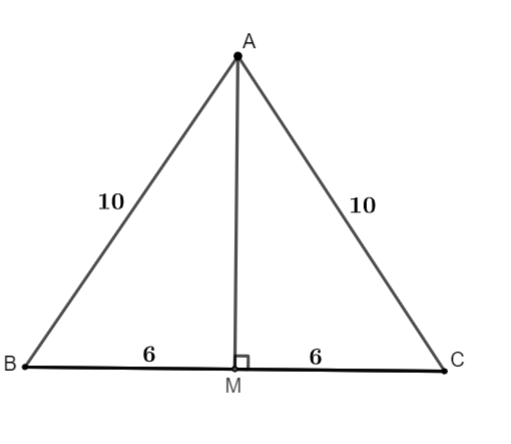Công thức lối trung tuyến

Ta sở hữu tam giác ABC cân nặng bên trên A, AM là trung tuyến suy rời khỏi AM là lối cao, lối phân giác của tam giác ABC

\Rightarrow BM = MC = \frac{1}{2}BC = 6

Áp dụng ấn định lý Pi – tớ – go cho tới tam giác vuông AMC có:

A{C^2} = A{M^2} + M{C^2} \Rightarrow AM = \sqrt {A{C^2} - M{C^2}} = 8

Xem thêm: Ai Sẽ Bên Em - Đinh Tùng Huy - NhacCuaTui

Ví dụ 2: Tính chừng lâu năm lối trung tuyến AM của tam giác ABC sở hữu góc , AB = 4cm, AC = 6cm.

Hướng dẫn giải

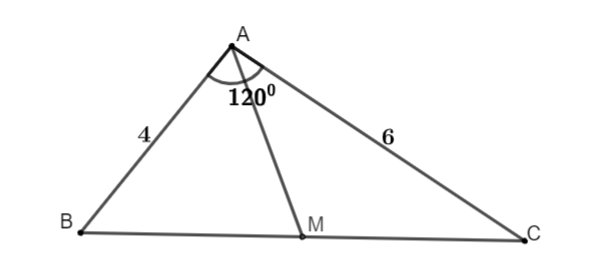Công thức lối trung tuyến

Ta có:

\begin{matrix} B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos {120^0} \hfill \\ \Rightarrow BC = 2\sqrt {19} \hfill \\ \Rightarrow A{M^2} = \dfrac{{A{B^2} + A{C^2}}}{2} - \dfrac{{B{C^2}}}{4} \hfill \\ \Rightarrow AM = \sqrt 7 \hfill \\ \end{matrix}

Ví dụ 3: Cho tam giác ABC vuông bên trên A có tính lâu năm hai tuyến đường trung tuyến AM và BN theo lần lượt vì thế 6cm và 9cm. Tính chừng lâu năm cạnh AB.

Hướng dẫn giải

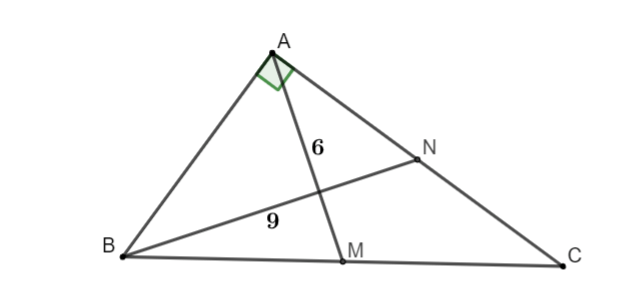
Công thức lối trung tuyến

Tam giác ABC vuông bên trên A, AM là trung tuyến nên AM = BM = MC = 6

Suy rời khỏi BC = 12

Mặt khác

\begin{matrix} \left\{ {\begin{array}{*{20}{c}} {A{M^2} = \dfrac{{A{B^2} + A{C^2}}}{2} - \dfrac{{B{C^2}}}{4}} \\ {B{N^2} = \dfrac{{B{C^2} + A{B^2}}}{2} - \dfrac{{A{C^2}}}{4}} \end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}} {\dfrac{{A{B^2} + A{C^2}}}{2} = 72} \\ {\dfrac{{A{B^2}}}{2} - \dfrac{{A{C^2}}}{4} = 45} \end{array}} \right. \hfill \\ \Rightarrow \left\{ {\begin{array}{*{20}{c}} {A{B^2} = 54} \\ {A{C^2} = 18} \end{array}} \right. \Rightarrow \left\{ {\begin{array}{*{20}{c}} {AB = 3\sqrt 6 } \\ {AC = 3\sqrt 2 } \end{array}} \right. \hfill \\ \hfill \\ \end{matrix}

D. Bài thói quen chừng lâu năm lối trung tuyến nhập tam giác

Bài 1: Tính chừng lâu năm lối trung tuyến AM của tam giác ABC sở hữu góc A = 120 chừng, AB = 4cm, AC = 6cm

Bài 2: Cho tam giác ABC sở hữu góc BAC vì thế 1200, AB = 2a, AC = 3a

a. Tính chừng lâu năm cạnh BC, lối trung tuyến AM

b. Tính nửa đường kính lối tròn xoe nước ngoài tiếp tam giác ABC

c. Gọi D là chân lối phân giác nhập góc ABC. Tính diện tích S tam giác BDA.

Bài 3: Cho tam giác MNP cân nặng bên trên M với lối trung tuyến MK (M ∈ NP)

a. Chứng minh tam giác MKN vì thế tam giác MKP

b. hiểu MN = MP = 13cm, NK = 5cm. Hãy tính chừng lâu năm lối trung tuyến MK

Xem thêm: Phim "Mai" của Trấn Thành dán nhãn 18+: Học sinh vẫn vô tư vào rạp?

Bài 4: Cho tam giác ABC sở hữu AB = 6cm, AC = 8cm, góc A = 60°

a. Tính chừng lâu năm cạnh BC, diện tích S và lối cao AH của tam giác

b. Tính nửa đường kính lối tròn xoe nội tiếp, nước ngoài tiếp tam giác ABC, chừng lâu năm trung tuyến BM của tam giác.

BÀI VIẾT NỔI BẬT

Tổng hợp cách tải phim trên web về iPhone nhanh, tiện lợi

Hiện nay, nhu cầu tải phim về điện thoại để xem khi offline ngày càng phổ biến, cho phép bạn dễ dàng thưởng thức những bộ phim hay video yêu thích mọi lúc, mọi nơi mà không cần có kết nối mạng, không cần truy cập website xem phim. Với người dùng đang sử dụng điện thoại iOS có thể...

Đặt vé máy bay giá rẻ 2024

Đặt vé máy bay giá rẻ nội địa và quốc tế tại Sanvemaybay.vn đơn giản và tiện lợi, bạn sẽ được trải nghiệm dịch vụ tuyệt vời.