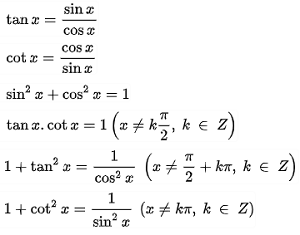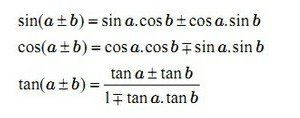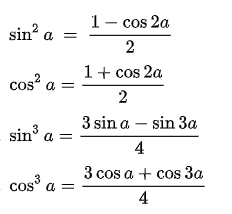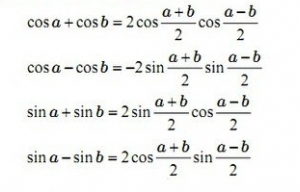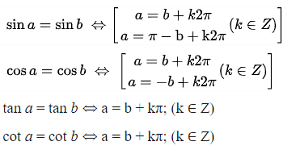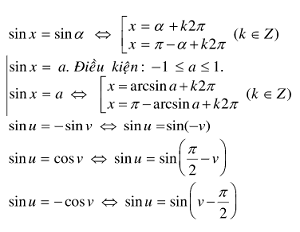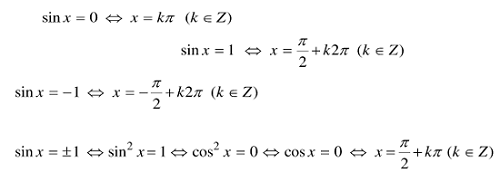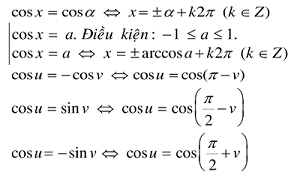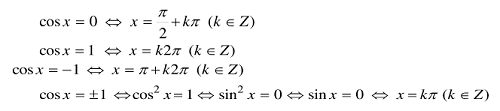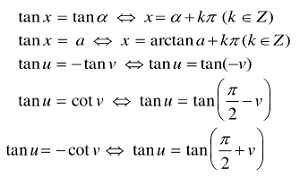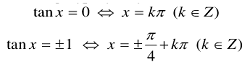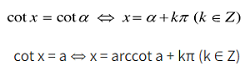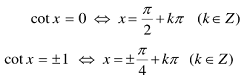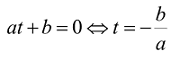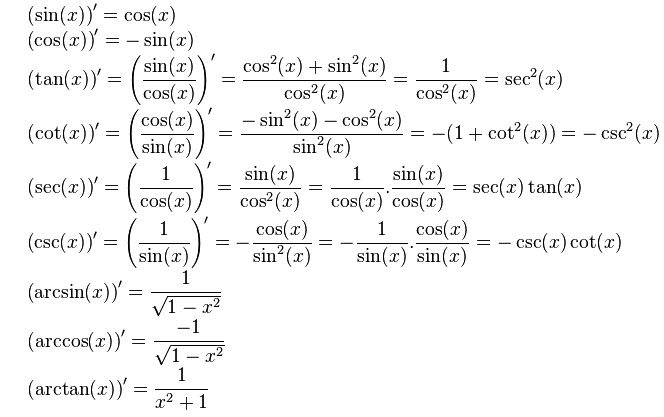Chi tiết lý thuyết và bài tập ứng dụng hàm số lượng giác, phương trình hàm số lượng giác trong toán học

Hàm con số giác là gì?

Các hàm lượng giác là những hàm toán học tập của góc, được sử dụng Khi phân tích tam giác và những hiện tượng kỳ lạ với đặc thù tuần trả. Các hàm lượng giác của một góc thông thường được khái niệm bởi tỷ trọng chiều nhiều năm nhị cạnh của tam giác vuông chứa chấp góc cơ, hoặc tỷ trọng chiều nhiều năm trong số những đoạn trực tiếp nối những điểm quan trọng bên trên vòng tròn trặn đơn vị chức năng. 

Bạn đang xem: Chi tiết lý thuyết và bài tập ứng dụng hàm số lượng giác, phương trình hàm số lượng giác trong toán học

Các công thức hàm con số giác vừa đủ nhất

Sau đó là những công thức hàm con số giác tuy nhiên chúng ta thông thường bắt gặp cần trong số kì đua, nhất là kì đua trung học phổ thông Quốc Gia.

Công thức hàm con số giác cơ bản

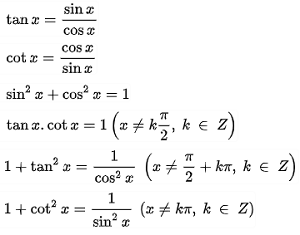
Công thức nằm trong vô hàm con số giác

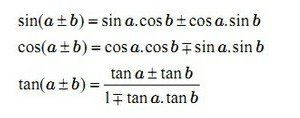
Mẹo dùng để làm lưu giữ nhanh chóng những công thức nằm trong vô hàm số là lời nói “Sin thì sin cos cos sin, cos thì cos cos sin sin lốt trừ. Tan thì tan nọ tan cơ phân chia mang lại hình mẫu số 1 trừ tan tan.”

Công thức những cung tương quan bên trên đàng tròn trặn lượng giác

Hai góc đối nhau:

• cos (-x) = cos x

• sin (-x) = -sin x

• tan (-x) = -tan x

• cot (-x) = -cot x

Hai góc bù nhau:

• sin (π - x) = sin x

• cos (π - x) = -cos x

• tan (π - x) = -tan x

• cot (π - x) = -cot x

Hai góc phụ nhau:

• sin (π/2 - x) = cos x

• cos (π/2 - x) = sin x

• tan (π/2 - x) = cot x

• cot (π/2 - x) = tan x

Hai góc rộng lớn thông thường π:

• sin (π + x) = -sin x

• cos (π + x) = -cos x

• tan (π + x) = tan x

• cot (π + x) = cot x

Hai góc rộng lớn thông thường π/2:

• sin (π/2 + x) = cos x

• cos (π/2 + x) = -sin x

• tan (π/2 + x) = -cot x

• cot (π/2 + x) = -tan x

Mẹo lưu giữ nhanh chóng công thức như sau: “Cos đối, sin bù, phụ chéo cánh, tan rộng lớn thông thường π.”

Công thức nhân

Công thức hạ bậc vô hàm con số giác

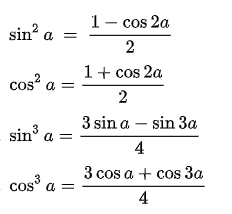
Công thức trở thành tổng trở thành tích

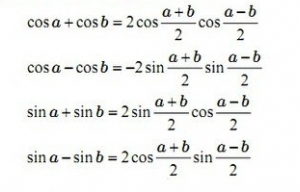
Mẹo canh ty dễ dàng và đơn giản ghi lưu giữ công thức hơn: “Cos nằm trong cos bởi 2 cos cos, cos trừ cos bởi trừ 2 sin sin; sin nằm trong sin bởi 2 sin cos, sin trừ sin bởi 2 cos sin.”

Công thức trở thành tích trở thành tổng

Nghiệm của phương trình lượng giác

Phương trình lượng giác cơ bản:

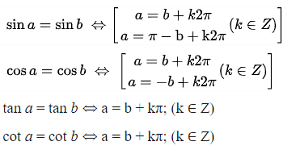
Phương trình lượng giác vô tình huống quánh biệt:

• sin a = 0 ⇔ a = kπ; (k ∈ Z)

• sin a = 1 ⇔ a = π/2 + k2π; (k ∈ Z)

• sin a = -1 ⇔ a = -π/2 + k2π; (k ∈ Z)

  Xem thêm: Vệ Sinh Máy Lạnh - Điện Máy Xanh Bảo Hành

• cos a = 0 ⇔ a = π/2 + kπ; (k ∈ Z)

• cos a = 1 ⇔ a = k2π; (k ∈ Z)

• cos a = -1 ⇔ a = π + k2π; (k ∈ Z)

Xem thêm: Khái niệm và công thức của số hữu tỉ, sự khác lạ thân ái số hữu tỉ và số vô tỉ là gì?

Phương trình lượng giác cơ phiên bản và những tình huống bịa biệt

Phương trình sin x = sin α, sin x = a

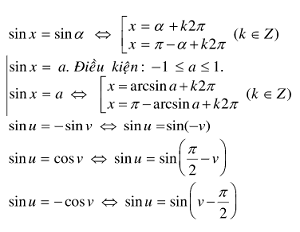
Các tình huống quánh biệt:

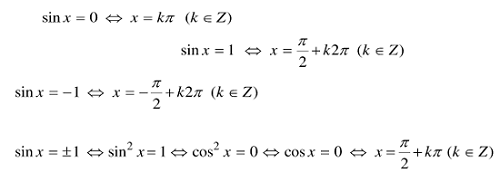
Phương trình cos x = cos α, cos x = a

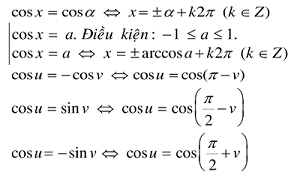
Các tình huống quánh biệt:

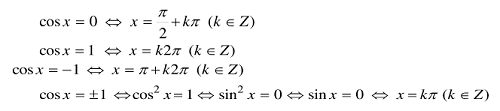
Phương trình tan x = tan α, tan x = a

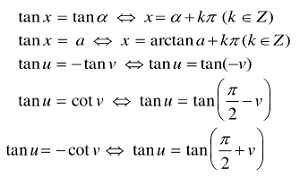
Các tình huống quánh biệt:

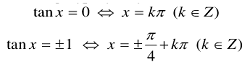
Phương trình cot x = cot α, cot x = a

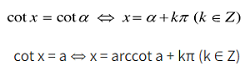
Các tình huống quánh biệt:

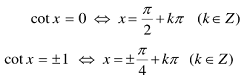
Phương trình số 1 so với một hàm con số giác

Có dạng at + b = 0 với a, b ∈ Ζ, a ≠ 0,với t là 1 hàm con số giác nào là cơ. Công thức giải như sau:

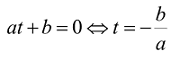
Đạo hàm hàm con số giác cơ bản

Đạo hàm của những hàm lượng giác là cách thức toán học tập mò mẫm vận tốc trở thành thiên của một hàm con số giác bám theo sự trở thành thiên của trở thành số. Các hàm con số giác thông thường bắt gặp là sin(x), cos(x) và tan(x).

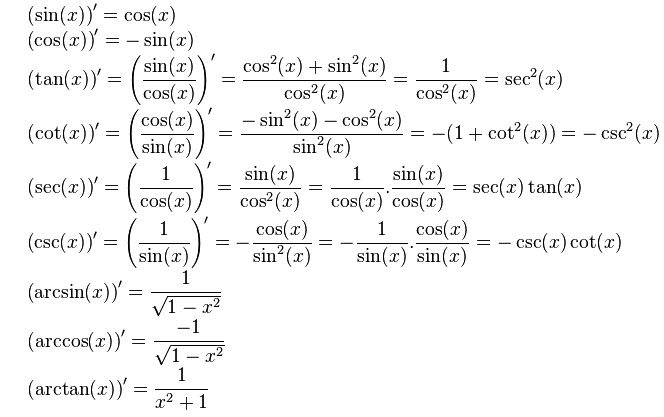
Cách tính số lượng giới hạn hàm con số giác hoặc nhất

Áp dụng số lượng giới hạn quánh biệt: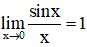

Các bước mò mẫm số lượng giới hạn hàm con số giác của 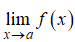 với f(x) là hàm con số giác

Bước 1: Sử dụng những công thức lượng giác cơ phiên bản, công thức nhân song, công thức nằm trong, công thức chuyển đổi,… nhằm chuyển đổi hàm con số giác f(x) về nằm trong dạng số lượng giới hạn quan trọng nêu bên trên.

Bước 2: gí dụng những lăm le lý về số lượng giới hạn nhằm mò mẫm số lượng giới hạn đang được mang lại.

Cách tính chu kỳ luân hồi hàm con số giác dễ dàng nắm bắt nhất

Hàm số y= f(x) xác lập bên trên tụ hội D được gọi là hàm số tuần trả nếu như với số T ≠ 0 sao mang lại với từng x ∈ D tớ với x+T ∈ D;x-T ∈ D và f(x+T)=f(x). Nếu với số T dương nhỏ nhất thỏa mãn nhu cầu những ĐK bên trên thì hàm số này được gọi là 1 hàm số tuần trả với chu kì T.

Cách mò mẫm chu kì của hàm con số giác (nếu có):

• Hàm số nó = k.sin(ax+b) với chu kì là T= 2π/|a|

• Hàm số y= k.cos(ax+ b) với chu kì là T= 2π/|a|

• Hàm số y= k.tan( ax+ b) với chu kì là T= π/|a|

• Hàm số y= k.cot (ax+ b ) với chu kì là: T= π/|a|

• Hàm số y= f(x) với chu kì T1; hàm số T2 với chu kì T2 thì chu kì của hàm số y= a.f(x)+ b.g(x) là T = bội công cộng nhỏ nhất của T1 và T2

Bài luyện mẫu:

Trong những hàm số tại đây, hàm số nào là là hàm số tuần hoàn?

A. y= sinx- x

B. y= cosx

C. y= x.sin x

D. y=(x2+1)/x

Đáp án: Chọn B

Tập xác lập của hàm số: D=R .

mọi x ∈ D , k ∈ Z tớ với x-2kπ ∈ D và x+2kπ ∈ D,cos(x+2kπ)=cosx .

Vậy y= cosx là hàm số tuần trả.

Xem thêm: Bức tranh BlackPink chibi đẹp đến tuyệt vời

Một số bài xích luyện tự động luyện về hàm con số giác

Trên đó là toàn bộ những vấn đề về hàm con số giác tuy nhiên bạn phải ghi lưu giữ. Hy vọng, với những share thực tiễn bên trên trên đây của Monkey, tiếp tục giúp cho bạn dễ dàng và đơn giản đoạt được những đề đua tiếp đây. Xin được sát cánh nằm trong chúng ta.