Cho hình chóp tam giác đều có cạnh bên bằng $\frac{{a\sqrt {21} }}{3}$ và mặt bên tạo với mặt phằng đáy một góc ${60^0}$?

Cho hình chóp tam giác đều sở hữu cạnh mặt mũi vì chưng $\frac{{a\sqrt {21} }}{3}$ và mặt mũi mặt tạo ra với mặt mũi phằng lòng một góc ${60^0}$?

Đáp án A

Chọn A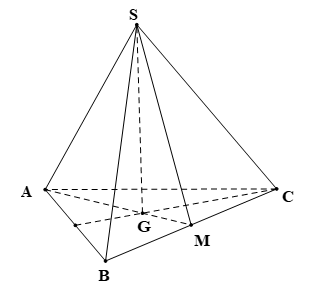

Giả sử chóp tam giác đều là \(S.ABC\), tao sở hữu tam giác \(ABC\) đều và \(SG \bot \left( {ABC} \right)\) với \(G\) là trọng tâm tam giác \(ABC\).
Gọi \(M\) là trung điểm của đoạn \(BC\), suy ra
\(\left\{ \begin{array}{l} AG \bot BC\\ SG \bot \left( {ABC} \right) \Rightarrow SG \bot BC \end{array} \right. \Rightarrow BC \bot \left( {SAG} \right) \Rightarrow BC \bot SM\).
Do bại \(\left( {\left( {SBC} \right),\left( {ABC} \right)} \right) = \left( {SM,AM} \right) = \widehat {SMA} = {60^0}\).
Gọi cạnh \(AB = x\left( {x > 0} \right)\), suy đi ra \(AM = \sqrt {A{B^2} - B{M^2}} = \dfrac{{x\sqrt 3 }}{2}\) \( \Rightarrow AG = \dfrac{2}{3}AM = \dfrac{{x\sqrt 3 }}{3}\);
\(GM = \dfrac{1}{3}AM = \dfrac{{x\sqrt 3 }}{6}\).
Lại sở hữu \(\tan \widehat {SMA} = \dfrac{{SG}}{{GM}} \Leftrightarrow \tan {60^0} = \dfrac{{SG}}{{GM}} \Leftrightarrow SG = GM.\tan {60^0} \Leftrightarrow SG = \dfrac{x}{2}\).
Mà tam giác \(SAG\) vuông bên trên \(G\) \( \Rightarrow S{G^2} + G{A^2} = S{A^2}\) \( \Leftrightarrow \dfrac{{{x^2}}}{4} + \dfrac{{{x^2}}}{3} = \dfrac{{7{a^2}}}{3} \Leftrightarrow {x^2} = 4{a^2} \Leftrightarrow x = 2a\).
Suy đi ra \(SG = a,{S_{\Delta ABC}} = \dfrac{1}{2}AM.BC = {a^2}\sqrt 3 \). Vậy \({V_{S.ABC}} = \dfrac{1}{3}.SG.{S_{\Delta ABC}} = \dfrac{{{a^3}\sqrt 3 }}{3}\).