Công thức viết phương trình đường phân giác hay chi tiết nhất | Toán lớp 10

Công thức viết lách phương trình đường phân giác hoặc cụ thể nhất - Toán lớp 10

Bạn đang xem: Công thức viết phương trình đường phân giác hay chi tiết nhất | Toán lớp 10

I. Lý thuyết tổ hợp.

- Tia phân giác của một góc: Là tia nằm trong lòng nhị cạnh của góc và tạo nên với nhị cạnh tê liệt nhị góc cân nhau.

- Đường phân giác của một góc: Là đường thẳng liền mạch chứa chấp tia phân giác của góc đó

- Tính chất: Mọi điểm phía trên lối phân giác của một góc đều cơ hội đều nhị cạnh của góc tê liệt, tức là khoảng cách kể từ điểm M bất kì phía trên lối phân giác của một góc cho tới nhị cạnh của góc là cân nhau.

II. Các công thức.

- Công thức viết lách phương trình đường phân giác của góc tạo nên bởi vì hai tuyến phố thẳng: Cho hai tuyến phố trực tiếp $d_1:a_{1}x+b_{1}y+c_1=0$  và $d_2:a_{2}x+b_{2}y+c_2=0$ .  Phương trình những lối phân giác của góc tạo nên bởi vì 2 đường thẳng liền mạch tê liệt là:

$\frac{a_{1}x+b_{1}y+c_1}{\sqrt{{a_1}^2+{b_1}^2}}=\pm \frac{a_{2}x+b_{2}y+c_2}{\sqrt{{a_2}^2+{b_2}^2}}$

- Chú ý: Cho đường thẳng liền mạch d: ax + by + c = 0 và nhị điểm $A(x_A;y_A)$ và $B(x_B;y_B)$không nằm trong d.

Đặt f(x; y) = ax + by + c

+ Nếu $f(x_A;y_A).f(x_B;y_B)>0\iff$ A và B ở và một phía so với d.

+ Nếu $f(x_A;y_A).f(x_B;y_B)<0\iff$ A và B ở không giống phía so với d.

III. Ví dụ minh họa.

Bài 1: Cho hai tuyến phố trực tiếp d: x + 2y + 3 = 0 và d’: 2x + nó + 3 = 0. Viết phương trình những lối phân giác của những góc tạo nên bởi vì d và d’.

Lời giải:

Phương trình những lối phân giác của những góc tạo nên bởi vì d và d’ là:

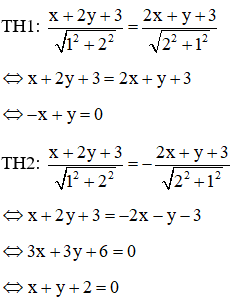
Vậy những phương trình đường phân giác của những góc tạo nên bởi vì hai tuyến phố trực tiếp d và d’ là $-x+y=0$ và $x+y+2=0$

Bài 2: Cho hai tuyến phố trực tiếp d: x - 2y + 1 = 0 và d’: 2x - nó + 2 = 0. Viết phương trình những lối phân giác của những góc tạo nên bởi vì d và d’.

Lời giải:

Xem thêm: Ứng dụng AI tạo ảnh anime gây sốt tại Việt Nam

Phương trình những lối phân giác của những góc tạo nên bởi vì d và d’ là:

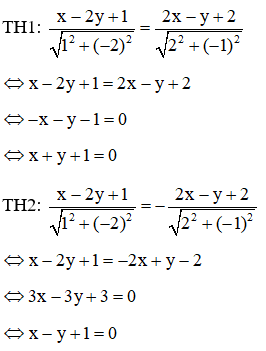
Vậy những phương trình đường phân giác của những góc tạo nên bởi vì hai tuyến phố trực tiếp d và d’ là $x+y+1=0$ và $x-y+1=0$.

Bài 3: Cho tam giác ABC đem đường thẳng liền mạch chứa chấp cạnh AB là d: 2x - nó + 4 = 0, đường thẳng liền mạch chứa chấp cạnh AC là d’: x - 2y - 6 = 0 và nhị điểm B, C nằm trong Ox. Viết phương trình phân giác ngoài của góc $\widehat{BAC}$.

Lời giải:

Phương trình lối phân giác của những góc tạo nên bởi vì d và d’ là:

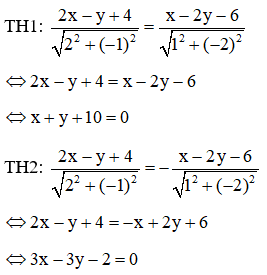
Do nhị điểm B và C nằm trong Ox và theo thứ tự nằm trong d và d’ nên tọa chừng nhị điểm này đó là : B(-2; 0) và C(6; 0).

Xét địa điểm của nhị điểm B và C so với đường thẳng liền mạch x + nó + 10 = 0.

Ta đem : (-2 + 0 + 10).( 6 + 0 + 10) > 0 nên nhị điểm B và C ở nằm trong phía đối với đường thẳng liền mạch x + nó + 10 = 0.

Suy đi ra đường thẳng liền mạch x + nó + 10 = 0 là lối phân giác ngoài của góc $\widehat{BAC}$ .

IV. Bài tập dượt tự động luyện

Bài 1: Viết phương trình những lối phân giác của những góc tạo nên bởi vì hai tuyến phố trực tiếp d: 3x – nó + 2 = 0 và   d’: x – 3y = 0.

Bài 2:  Viết phương trình những lối phân giác của những góc tạo nên bởi vì hai tuyến phố trực tiếp d: 2x – 3y + 8 = 0 và   d’: 3x – 2y – 5 = 0.

Xem tăng tổ hợp công thức môn Toán lớp 10 không thiếu thốn và cụ thể khác:

Công thức viết lách phương trình đường thẳng liền mạch bám theo đoạn chắn hoặc, cụ thể nhất 

Công thức thám thính điểm đối xứng qua loa đường thẳng liền mạch hoặc và chi tiết 

Xem thêm: [ Tập Hợp] Những thông tin cần biết về Bệnh viện E

Công thức về địa điểm kha khá của hai tuyến phố trực tiếp hoặc và cụ thể nhất 

Công thức tính góc thân thích hai tuyến phố trực tiếp hoặc, cụ thể nhất 

Công thức tính khoảng cách từ là 1 điểm đến chọn lựa một lối thẳng