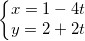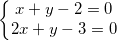Trong công tác toán lớp 10, nội dung về phương trình đàng thắng nhập mặt mày phẳng lì cũng đều có một số trong những dạng toán khá hoặc, tuy vậy, những dạng toán này nhiều khi thực hiện không hề ít các bạn lầm lẫn công thức khi áp dụng giải bài bác luyện.
Vì vậy, nhập nội dung bài viết này tất cả chúng ta nằm trong hệ thống lại những dạng toán về phương trình đường thẳng liền mạch nhập mặt mày phẳng lì và giải những bài bác luyện minh hoạ mang đến từng dạng toán nhằm những em đơn giản dễ dàng thâu tóm kiến thức và kỹ năng tổng quát tháo của đường thẳng liền mạch.
Bạn đang xem: Các dạng toán về phương trình đường thẳng trong mặt phẳng, bài tập vận dụng - Toán lớp 10
» Đừng vứt lỡ: Tổng phù hợp những dạng toán phương trình đàng tròn trĩnh đặc biệt hay
I. Tóm tắt lý thuyết phương trình đàng thẳng
1. Vectơ pháp tuyến và phương trình tổng quát tháo của đàng thẳng
a) Vectơ pháp tuyến của đàng thẳng
- Cho đường thẳng liền mạch (d), vectơ 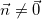 gọi là vectơ pháp tuyến (VTPT) của (d) nếu như giá chỉ của
gọi là vectơ pháp tuyến (VTPT) của (d) nếu như giá chỉ của  vuông góc với (d).
vuông góc với (d).
* Nhận xét: Nếu 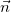 là vectơ pháp tuyến của (d) thì
là vectơ pháp tuyến của (d) thì 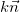 cũng là VTPT của (d).
cũng là VTPT của (d).
b) Phương trình tổng quát tháo của đàng thẳng
* Định nghĩa
- Phương trình (d): ax + by + c = 0, nhập bại a và b ko bên cạnh đó vày 0 tức là (a2 + b2 ≠ 0) là phương trình tổng quát tháo của đường thẳng liền mạch (d) nhận 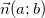 là vectơ pháp tuyến.
là vectơ pháp tuyến.
* Các dạng đặc trưng của phương trình đường thẳng liền mạch.
- (d): ax + c = 0 (a ≠ 0): (d) tuy vậy song hoặc trùng với Oy
- (d): by + c = 0 (b ≠ 0): (d) tuy vậy song hoặc trùng với Ox
- (d): ax + by = 0 (a2 + b2 ≠ 0): (d) trải qua gốc toạ phỏng.
- Phương trình dạng đoạn chắn: ax + by = 1 nên (d) trải qua A (a;0) B(0;b) (a,b ≠ 0)
- Phương trình đàng thẳng có thông số góc k: y= kx+m (k được gọi là thông số góc của đàng thẳng).
2. Vectơ chỉ phương và phương trình thông số, phương trình chủ yếu tắc của đàng thẳng
a) Vectơ chỉ phương của đàng thẳng
- Cho đường thẳng liền mạch (d), vectơ 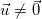 gọi là vectơ chỉ phương (VTCP) của (d) nếu như giá chỉ của
gọi là vectơ chỉ phương (VTCP) của (d) nếu như giá chỉ của 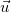 song tuy vậy hoặc trùng với (d).
song tuy vậy hoặc trùng với (d).
* Nhận xét: Nếu 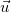 là vectơ chỉ phương của (d) thì
là vectơ chỉ phương của (d) thì 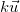 cũng là VTCP của (d). VTCP và VTPT vuông góc cùng nhau, chính vì vậy nếu như (d) đem VTCP
cũng là VTCP của (d). VTCP và VTPT vuông góc cùng nhau, chính vì vậy nếu như (d) đem VTCP 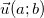 thì
thì 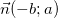 là VTPT của (d).
là VTPT của (d).
b) Phương trình thông số của đàng thẳng:
* đem dạng: 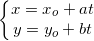 ; (a2 + b2 ≠ 0) đường thẳng liền mạch (d) trải qua điểm M0(x0;y0) và nhận
; (a2 + b2 ≠ 0) đường thẳng liền mạch (d) trải qua điểm M0(x0;y0) và nhận 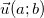 làm vectơ chỉ phương, t là thông số.
làm vectơ chỉ phương, t là thông số.
* Chú ý: - Khi thay cho từng t ∈ R nhập PT thông số tao được một điểm M(x;y) ∈ (d).
- Nếu điểm M(x;y) ∈ (d) thì sẽ sở hữu được một t sao mang đến x, nó thoả mãn PT thông số.
- 1 đường thẳng liền mạch sẽ sở hữu được vô số phương trình thông số (vì ứng với mỗi t ∈ R tao có một phương trình tham lam số).
c) Phương trình chủ yếu tắc của đàng thẳng
* đem dạng: 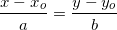 ; (a,b ≠ 0) đường trực tiếp (d) trải qua điểm M0(x0;y0) và nhận
; (a,b ≠ 0) đường trực tiếp (d) trải qua điểm M0(x0;y0) và nhận 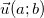 làm vectơ chỉ phương.
làm vectơ chỉ phương.
d) Phương trình đường thẳng liền mạch trải qua 2 điểm
- Phương trình đường thẳng liền mạch trải qua 2 điểm A(xA;yA) và B(xB;yB) đem dạng:
+ Nếu: 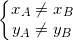 thì đường thẳng liền mạch qua loa AB đem PT chủ yếu tắc là:
thì đường thẳng liền mạch qua loa AB đem PT chủ yếu tắc là: 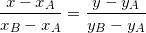
+ Nếu: xA = xB: ⇒ AB: x = xA
+ Nếu: yA = yB: ⇒ AB: nó = yA
e) Khoảng cơ hội từ là 1 điểm cho tới 1 đàng thẳng
- Cho điểm M(x0;y0) và đàng thẳng Δ: ax + by + c = 0, khoảng cách kể từ M đến Δ được xem theo đòi công thức sau:
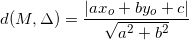
3. Vị trí kha khá của 2 đàng thẳng
- Cho 2 đường thẳng liền mạch (d1): a1x + b1y + c1 = 0; và (d2): a2x + b2y + c =0;
+ d1 cắt d2 ⇔ 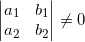
+ d1 // d2 ⇔ 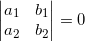 và
và 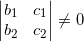 hoặc
hoặc 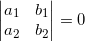 và
và 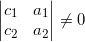
+ d1 ⊥ d2 ⇔ 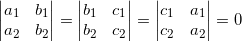
* Lưu ý: nếu a2.b2.c2 ≠ 0 thì:
- Hai đường thẳng liền mạch tách nhau nếu: 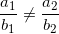
- Hai đường thẳng liền mạch // nhau nếu: 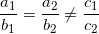
- Hai đàng thẳng ⊥ nhau nếu: 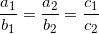

II. Các dạng toán về phương trình đàng thẳng
Dạng 1: Viết phương trình đường thẳng liền mạch lúc biết vectơ pháp tuyến và một điểm nằm trong đàng thẳng
Ví dụ: Viết PT tổng quát tháo của đường thẳng liền mạch (d) biết (d): trải qua điểm M(1;2) và đem VTPT 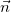 = (2;-3).
= (2;-3).
* Lời giải: Vì (d) trải qua điểm M(1;2) và đem VTPT 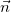 = (2;-3)
= (2;-3)
⇒ PT tổng quát tháo của đường thẳng liền mạch (d) là: 2(x-1) - 3(y-2) = 0 ⇔ 2x - 3y +4 = 0
» xem tăng ví dụ: Viết phương trình đường thẳng liền mạch cút sang một điểm đem vectơ pháp tuyến n
Dạng 2: Viết phương trình đường thẳng liền mạch lúc biết vectơ chỉ phương và một điểm nằm trong đàng thẳng
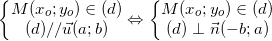

Ví dụ: Viết phương trình đường thẳng liền mạch (d) hiểu được (d) trải qua điểm M(-1;2) và đem VTCP 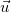 = (2;-1)
= (2;-1)
* Lời giải: Vì đường thẳng liền mạch đi qua loa M (1 ;-2) và đem vtcp là 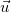 = (2;-1)
= (2;-1)
⇒ phương trình thông số của đường thẳng liền mạch là : 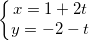
» xem tăng ví dụ: Viết phương trình đường thẳng liền mạch cút sang một điểm đem vectơ chỉ phương u
Dạng 3: Viết phương trình đường thẳng liền mạch cút sang một điểm và tuy vậy song với một đàng thẳng
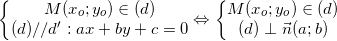
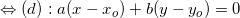
Ví dụ: Viết phương trình đường thẳng liền mạch (d) biết rằng:
a) trải qua M(3;2) và //Δ: 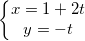
b) trải qua M(3;2) và //Δ: 2x - nó - 1 = 0
* Lời giải:
a) Đường thẳng Δ đem VTCP 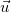 = (2;-1) vì như thế (d) // Δ nên (d) nhận
= (2;-1) vì như thế (d) // Δ nên (d) nhận 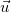 = (2;-1) là VTCP, (d) qua loa M(3;2)
= (2;-1) là VTCP, (d) qua loa M(3;2)
⇒ PT đường thẳng liền mạch (d) là: 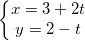
b) đường trực tiếp Δ: 2x – nó – 1 = 0 đem vtpt là 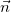 = (2;-1). Đường trực tiếp (d) //Δ nên
= (2;-1). Đường trực tiếp (d) //Δ nên 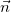 = (2;-1) cũng chính là VTPT của (d).
= (2;-1) cũng chính là VTPT của (d).
⇒ PT (d) trải qua điểm M(3;2) và đem VTPT 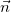 = (2;-1) là:
= (2;-1) là:
2(x-3) - (y-2) = 0 ⇔ 2x - nó -4 = 0
» xem tăng ví dụ: Viết phương trình đường thẳng liền mạch cút sang một điểm và tuy vậy song với một đàng thẳng
Dạng 4: Viết phương trình đường thẳng liền mạch cút sang một điểm và vuông góc với một đàng thẳng

Ví dụ: Viết phương trình đường thẳng liền mạch (d) hiểu được (d):
a) trải qua M(-2;3) và ⊥ Δ: 2x - 5y + 3 = 0
b) trải qua M(4;-3) và ⊥ Δ: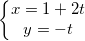
* Lời giải:
a) Đường thẳng Δ: 2x - 5y + 3 = 0 nên Δ đem VTPT là 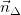 =(2;-5)
=(2;-5)
vì (d) vuông góc với Δ nên (d) nhận VTPT của Δ thực hiện VTCP ⇒ 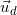 = (2;-5)
= (2;-5)
⇒ PT (d) trải qua M(-2;3) đem VTCP 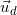 = (2;-5) là:
= (2;-5) là: 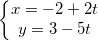
Xem thêm: Ăn ngon với 9 quán lòng nướng Hà Nội chuẩn vị, bao sạch
b) Đường thẳng Δ đem VTCP 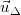 = (2;-1), vì như thế d⊥ Δ nên (d) nhận VTCP
= (2;-1), vì như thế d⊥ Δ nên (d) nhận VTCP 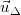 làm VTPT ⇒
làm VTPT ⇒ 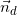 = (2;-1)
= (2;-1)
⇒ Vậy (d) trải qua M(4;-3) đem VTPT 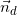 = (2;-1) đem PTTQ là:
= (2;-1) đem PTTQ là:
2(x-4) - (y+3) = 0 ⇔ 2x - nó - 11 = 0.
» xem tăng ví dụ: Viết phương trình đường thẳng liền mạch cút sang một điểm và vuông góc với một đàng thẳng
Dạng 5: Viết phương trình đường thẳng liền mạch trải qua 2 điểm
- Đường trực tiếp trải qua 2 điểm A và B đó là đường thẳng liền mạch trải qua A nhận nhận vectơ 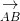 làm vectơ chỉ phương (trở về dạng toán 2).
làm vectơ chỉ phương (trở về dạng toán 2).
Ví dụ: Viết PTĐT trải qua 2 điểm A(1;2) và B(3;4).
* Lời giải:
- Vì (d) trải qua 2 điểm A, B nên (d) đem VTCP là: 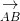 = (3-1;4-2) = (2;2)
= (3-1;4-2) = (2;2)
⇒ Phương trình thông số của (d) là: 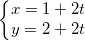
» xem tăng ví dụ: Viết phương trình đường thẳng liền mạch trải qua 2 điểm A, B
Dạng 6: Viết phương trình đường thẳng liền mạch cút sang một điểm và đem thông số góc k mang đến trước
- (d) đem dạng: nó = k(x-x0) + y0
Ví dụ: Viết PTĐT (d) trải qua M(-1;2) và đem thông số góc k = 3;
* Lời giải:
- PTĐT (d) trải qua M(-1;2) và đem thông số góc k = 3 đem dạng: y = k(x-x0) + y0
⇒ Vậy PTĐT (d) là: nó = 3(x+1) + 2 ⇔ nó = 3x + 5.
» xem tăng ví dụ: Viết phương trình đường thẳng liền mạch cút sang một điểm và đem thông số góc k
Dạng 7: Viết phương trình đàng trung trực của một quãng thẳng
- Trung trực của đoạn trực tiếp AB đó là đường thẳng liền mạch trải qua trung điểm I của đoạn trực tiếp này và nhận vectơ 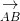 làm VTPT (trở về dạng toán 1).
làm VTPT (trở về dạng toán 1).
Ví dụ: Viết PTĐT (d) vuông góc với đường thẳng liền mạch AB và trải qua trung tuyến của AB biết: A(3;-1) và B(5;3)
* Lời giải:
- (d) vuông góc với AB nên nhận 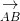 = (2;4) thực hiện vectơ pháp tuyến
= (2;4) thực hiện vectơ pháp tuyến
- (d) trải qua trung điểm I của AB, và I đem toạ độ:
xi = (xA+xB)/2 = (3+5)/2 = 4;
yi = (yA+yB)/2 = (-1+3)/2 = 1;
⇒ toạ phỏng của I(4;1)
⇒ (d) trải qua I(4;1) đem VTPT (2;4) đem PTTQ là:
2(x-4) + 4(y-1) = 0
⇔ 2x + 4y -12 = 0
⇔ x + 2y - 6 = 0.
» xem tăng ví dụ: Viết phương trình đàng trung trực của một đoạn thẳng
Dạng 8: Viết phương trình đường thẳng liền mạch cút sang một điểm và tạo nên với Ox 1 góc ∝ mang đến trước
- (d) trải qua M(x0;y0) và tạo nên với Ox 1 góc ∝ (00 < ∝ < 900) có dạng: nó = k(x-x0) + y0 (với k = ±tan∝
Ví dụ: Viết PTĐT (d) biết (d) trải qua M(-1;2) và tạo nên với chiều dương trục Ox 1 góc vày 450.
* Lời giải:
- Giả sử đường thẳng liền mạch (d) đem thông số góc k, như vây k được mang đến bở công thức:
k = tan∝ = tan(450) = 1.
⇒ PTĐT (d) trải qua M(-1;2) và đem thông số góc k = 1 là:
y = 1.(x+1) + 2 ⇔ nó = x + 3
Dạng 9: Tìm hình chiếu vuông góc của một điểm lên 1 đàng thẳng
* Giải sử cần thiết tìm hiểu hình chiếu H của điểm M lên đường thẳng liền mạch (d), tao thực hiện như sau:
- Lập phương trình đường thẳng liền mạch (d') qua loa M vuông góc với (d). (theo dạng toán 4).
- H là hình chiếu vuông góc của M lên (d) ⇒ H là gửi gắm của (d) và (d').
Ví dụ: Tìm hình chiếu của điểm M(3;-1) lên đường thẳng liền mạch (d) đem PT: x + 2y - 6 = 0
* Lời giải:
- Gọi (d') là đường thẳng liền mạch trải qua M và vuông góc với (d)
- (d) đem PT: x + 2y - 6 = 0 nên VTPT của (d) là: 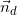 = (1;2)
= (1;2)
- (d') ⊥ (d) nên nhận VTPT của (d) là VTCP ⇒ 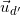 =(1;2)
=(1;2)
- PTĐT (d') qua loa M(3;-1) đem VTCP (1;2) là: 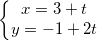
- H là hình chiếu của M thì H là gửi gắm điểm của (d) và (d') nên có:
Thay x,nó kể từ (d') và PT (d): (3+t) + 2(-1+2t) - 6 = 0 ⇔ 5t - 5 = 0 ⇔ t =1
⇒ x = 4, nó = một là toạ phỏng điểm H.
» xem tăng ví dụ: Cách tìm hiểu hình chiếu vuông góc của một điểm lên đường thẳng liền mạch nhập Oxy
Dạng 10: Tìm điểm đối xứng của một điểm qua loa một đàng thẳng
* Giải sử cần thiết tìm hiểu điểm M' đối xứng với M qua loa (d), tao thực hiện như sau:
- Tìm hình chiếu H của M lên (d). (theo dạng toán 9).
- M' đối xứng với M qua loa (d) nên M' đối xứng với M qua loa H (khi bại H là trung điểm của M và M').
Ví dụ: Tìm điểm M' đối xứng với M(3;-1) qua loa (d) đem PT: x + 2y - 6 = 0
* Lời giải:
- Đầu tiên tao tìm hiểu hình chiếu H của M(3;-1) lên (d). Theo ví dụ ở dạng 9 tao đem H(4;1)
- Khi bại H là trung điểm của M(3;-1) và M'(xM';yM'), tao có:
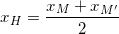 ;
; 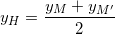
⇒ xM' = 2xH - xM = 2.4 - 3 = 5
⇒ yM' = 2yH - yM = 2.1 - (-1) = 3
⇒ Điểm đối xứng của M(3;-1) lên (d): x + 2y - 6 = 0 là M'(5;3)
» xem tăng ví dụ: Cách tìm hiểu điểm đối xứng của một điểm qua loa đàng thẳng
Dạng 11: Xác xác định trí kha khá của 2 đàng thẳng
- Để xét địa điểm của 2 đường thẳng liền mạch (d1): a1x + b1y + c1 = 0; và (d2): a2x + b2y + c =0; tao giải hệ phương trình:
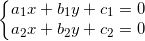 (*)
(*)
_ Hệ (*) vô nghiệm ⇒ d1 // d2
_ Hệ (*) vô số nghiệm ⇒ d1 ≡ d2
_ Hệ (*) có nghiệm duy nhất ⇒ d1 cắt d2 và nghiệm là toạ phỏng gửi gắm điểm.
Ví dụ: Xét địa điểm kha khá của 2 đàng thằng
a) d1: x + nó - 2 = 0; d2: 2x + nó - 3 = 0
b) d1: x + 2y - 5 = 0; d2: 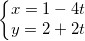
* Lời giải:
a) Số gửi gắm điểm của d1 và d2 là số nghiệm của hệ phương trình
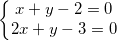
- Giải hệ PT bên trên tao được nghiệm x = 1; nó =1.
Xem thêm: Tuyển chọn 700+ ảnh trai đẹp Trung Quốc ngầu với phong cách đậm chất thể thao và hiện đại
b) Từ PTĐT d2 tao đem x = 1-4t và nó = 2+2t thay cho nhập PTĐT d1 tao được:
(1-4t) + 2(2+2t) - 5 = 0 ⇔ 0 = 0 ⇒ 2 đường thẳng liền mạch trùng nhau (có vô số nghiệm).
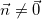 gọi là vectơ pháp tuyến (VTPT) của (d) nếu như giá chỉ của
gọi là vectơ pháp tuyến (VTPT) của (d) nếu như giá chỉ của 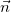 vuông góc với (d).
vuông góc với (d).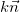 cũng là VTPT của (d).
cũng là VTPT của (d).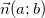 là vectơ pháp tuyến.
là vectơ pháp tuyến.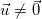 gọi là vectơ chỉ phương (VTCP) của (d) nếu như giá chỉ của
gọi là vectơ chỉ phương (VTCP) của (d) nếu như giá chỉ của 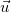 song tuy vậy hoặc trùng với (d).
song tuy vậy hoặc trùng với (d).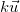 cũng là VTCP của (d). VTCP và VTPT vuông góc cùng nhau, chính vì vậy nếu như (d) đem VTCP
cũng là VTCP của (d). VTCP và VTPT vuông góc cùng nhau, chính vì vậy nếu như (d) đem VTCP 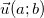 thì
thì 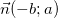 là VTPT của (d).
là VTPT của (d).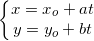 ; (a2 + b2 ≠ 0) đường thẳng liền mạch (d) trải qua điểm M0(x0;y0) và nhận
; (a2 + b2 ≠ 0) đường thẳng liền mạch (d) trải qua điểm M0(x0;y0) và nhận 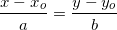 ; (a,b ≠ 0) đường trực tiếp (d) trải qua điểm M0(x0;y0) và nhận
; (a,b ≠ 0) đường trực tiếp (d) trải qua điểm M0(x0;y0) và nhận 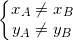 thì đường thẳng liền mạch qua loa AB đem PT chủ yếu tắc là:
thì đường thẳng liền mạch qua loa AB đem PT chủ yếu tắc là: 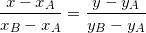
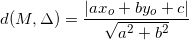
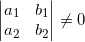
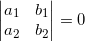 và
và 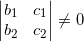 hoặc
hoặc 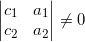
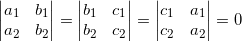
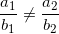
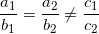
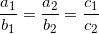

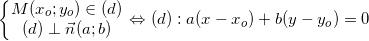
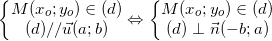

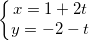
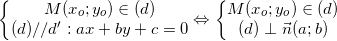
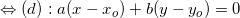
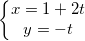
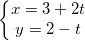
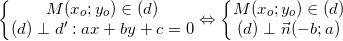
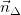 =(2;-5)
=(2;-5)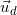 = (2;-5)
= (2;-5)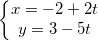
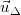 = (2;-1), vì như thế d⊥ Δ nên (d) nhận VTCP
= (2;-1), vì như thế d⊥ Δ nên (d) nhận VTCP 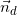 = (2;-1)
= (2;-1)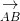 làm vectơ chỉ phương (trở về dạng toán 2).
làm vectơ chỉ phương (trở về dạng toán 2).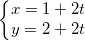
 = (1;2)
= (1;2) =(1;2)
=(1;2)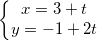
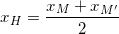 ;
; 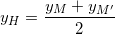
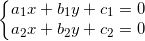 (*)
(*)