benhhocmatngu
benhhocmatngu
Trang chủ Uncategorized Công thức tính đường cao trong tam giác (2024) và bài tập có đáp án

Công thức tính đường cao trong tam giác (2024) và bài tập có đáp án

Với tư liệu về Công thức tính lối cao nhập tam giác (2024) và bài bác tập dượt với đáp án gồm những: lý thuyết và bài bác tập dượt cũng tựa như các khái niệm, đặc thù, những dạng bài bác tiếp tục giúp đỡ bạn nắm rõ kỹ năng và học tập chất lượng môn Toán rộng lớn.

Công thức tính lối cao nhập tam giác (2024) và bài bác tập dượt với đáp án

Bạn đang xem: Công thức tính đường cao trong tam giác (2024) và bài tập có đáp án

I. Lý thuyết

Đường cao của tam giác là đoạn vuông góc kẻ từ là một đỉnh cho tới cạnh đối lập. Cạnh đối lập này được gọi là lòng ứng với lối cao. Độ lâu năm của lối cao là khoảng cách thân ái đỉnh và lòng.

  • Cạnh đối lập được gọi là lòng ứng với lối cao ê.
  • Giao điểm thân ái lòng và lối cao được gọi là chân của lối cao.
  • Độ lâu năm của lối cao được xem vày khoảng cách kể từ đỉnh cho tới lòng.
  • Trong một tam giác sẽ có được 3 lối cao được hạ kể từ 3 đỉnh của tam giác ê. Ba lối cao này tiếp tục đồng quy (giao nhau) bên trên một điểm. Điểm này được gọi là trực tâm.
  • Trực tâm của tam giác rất có thể ở trong (xuất hiện nay ở tam giác nhọn) hoặc ở ngoài (ở tam giác tù) hoặc trùng với cùng 1 đỉnh nhập tam giác (xuất hiện nay ở tam giác vuông).

II. Công thức tính lối cao nhập tam giác

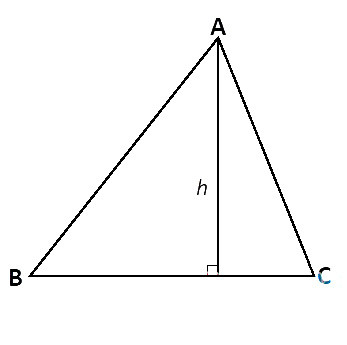
1. Công thức tính lối cao nhập tam giác thường

Có vô số cách chung chúng ta tính lối cao, cơ hội giản dị và đơn giản tính lối cao nhập tam giác là dùng công thức Heron:

{h_a} = 2\frac{{\sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} }}{a}

Với a, b, c là chừng lâu năm những cạnh; ha là lối cao được kẻ kể từ đỉnh A xuống cạnh BC; p là nửa chu vi:

p = \frac{{\left( {a + b + c} \right)}}{2}

Công thức tính lối cao nhập tam giác (2024) và bài bác tập dượt với đáp án (ảnh 1)

2. Công thức tính lối cao nhập tam giác đều

Giả sử tam giác đều ABC có tính lâu năm cạnh vày a như sau:

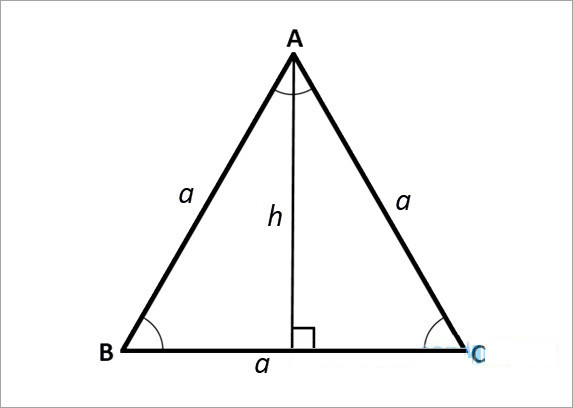
Công thức tính lối cao nhập tam giác (2024) và bài bác tập dượt với đáp án (ảnh 1)

Công thức tính lối cao: h = a\frac{{\sqrt 3 }}{2}

Trong đó: h là lối cao của tam giác đều; a là chừng lâu năm cạnh của tam giác đều.

3. Công thức tính lối cao nhập tam giác vuông

Giả sử với tam giác vuông ABC vuông bên trên A như hình sau:

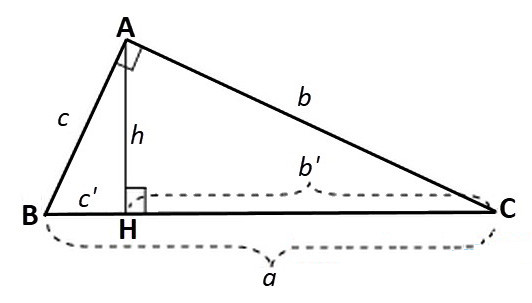
Công thức tính lối cao nhập tam giác (2024) và bài bác tập dượt với đáp án (ảnh 1)

Công thức tính cạnh và lối cao nhập tam giác vuông:

1.\ {a^2} = {b^2} + {c^2}

2.\ {b^2} = a.b' và {c^2} = a.c'

3.\ ah = bc

4.\ {h^2} = b'.c'

5.\ \frac{1}{{{h^2}}} = \frac{1}{{{b^2}}} + \frac{1}{{{c^2}}}

Trong đó: a, b, c theo thứ tự là những cạnh của tam giác vuông như hình trên;

b’ là lối chiếu của cạnh b bên trên cạnh huyền; c’ là lối chiếu của cạnh c bên trên cạnh huyền;

h là độ cao của tam giác vuông được kẻ kể từ đỉnh góc vuông A xuống cạnh huyền BC.

Ví dụ:

Cho tam giác ABC vuông bên trên A, AB=24cm, AC=32cm. Đường trung trực của BC hạn chế AC, BC theo đuổi trật tự D và E. Tính DE.

Giải:

Xét tam giác vuông ABC, tao có:

BC2 = AB2+ AC2 ( theo đuổi quyết định lý py-ta-go)

BC2 = 242+ 322

Xem thêm: [ Tập Hợp] Những thông tin cần biết về Bệnh viện E

BC2 = 1600

BC = 40(cm)

EC = BC : 2 = 40 : 2 = 20(cm)

Xét tam giác vuông Ngân Hàng Á Châu và tam giác vuông ECD có:

Có ∠A = ∠E = 90o

∠C chung

=> Tam giác Ngân Hàng Á Châu ∾ tam giác ECD (g.g)

=> AC/EC = AB/ED

=> ED = AB.EC/AC = 15cm

Vậy ED = 15cm

4. Công thức tính lối cao nhập tam giác cân

Giả sử chúng ta với tam giác ABC cân nặng bên trên A, lối cao AH vuông góc bên trên H như sau:

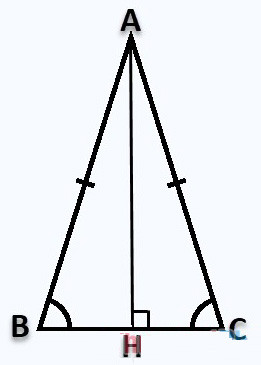
Công thức tính lối cao nhập tam giác (2024) và bài bác tập dượt với đáp án (ảnh 1)

Công thức tính lối cao AH:

Vì tam giác ABC cân nặng bên trên A nên lối cao AH đôi khi là lối trung tuyến nên:

\Rightarrow HB = HC = \frac{{BC}}{2}

Áp dụng quyết định lý Pytago nhập tam giác vuông ABH vuông bên trên H tao có:

A{H^2} + B{H^2} = A{B^2}

\Rightarrow A{H^2} = A{B^2} - B{H^2}

5. Tính hóa học phụ vương lối cao của một tam giác

Ba lối cao của tam giác nằm trong trải qua một điểm. Điểm ê gọi là trực tâm của tam giác.

III. Bài tập dượt vận dụng

Bài 1: Cho tam giác ABC lối cao AH. Vẽ HD ⊥ AB. Tia phân giác của góc AHC hạn chế AC bên trên F. thạo AB = 6cm, AC = 8cm, BC = 10 centimet. Tính:

a) Độ lâu năm AH

b) Chu vi tam giác ADF

Bài 2: Cho tam giác ABC vuông bên trên A, AB : AC = 7 : 24, BC = 625 centimet. Tính chừng lâu năm hình chiếu của nhị cạnh góc vuông bên trên cạnh huyền.

Bài 3: Cho tam giác ABC vuông bên trên A, lối cao AH. thạo AC = đôi mươi centimet, BH = 9cm. Tính chừng lâu năm BC và AH

Bài 4: Cho tam giác ABC vuông bên trên A, lối cao AH. thạo AB/AC = 20/21 và AH = 420. Tính chu vi tam giác ABC

Bài 5: Cho tam giác ABC vuông bên trên A, lối cao AH

Cho biết AC/AB = √2; HC - HB = 2cm.Tính:

Xem thêm: Đặt vé máy bay từ Sài Gòn đi Phú Quốc

a) Tỉ số HC : HB

b) Các cạnh của tam giác ABC

Bài 6: Cho tam giác nhọn ABC, hai tuyến phố cao BD và CE hạn chế nhau bên trên H. Trên HB, HC theo thứ tự lấy những điểm M, N sao mang đến góc AMC vày góc ANB vày 900. Chứng minh rằng AM = AN

BÀI VIẾT NỔI BẬT

Chi tiết lý thuyết và bài tập ứng dụng hàm số lượng giác, phương trình hàm số lượng giác trong toán học

Bài viết này của Monkey sẽ chia sẻ chi tiết các kiến thức từ cơ bản đến nâng cao của hàm số lượng giác trong toán học. Việc này sẽ giúp bạn dễ dàng tổng hợp, cũng như ghi nhớ tốt hơn các kiến thức đã học trên trường lớp.

Cách tải Zoom Cloud Meeting về máy tính, laptop ai cũng làm được

Nhu cầu hội họp và mở lớp học trực tuyến của mọi người ngày càng trở nên phổ biến. Và ứng dụng Zoom Cloud Meeting cũng ngày càng được sử dụng rộng rãi hơn nhờ lý do đó. Cách tải Zoom Cloud Meeting về máy tính, laptop cũng vô cùng dễ dàng, tìm hiểu ngay cùng GEARVN nhé!