Chủ đề: lăm le lý viet bậc 3: Định lí Vi-ét cho tới phương trình bậc tía là 1 trong những trong mỗi trở nên tựu toán học tập xứng đáng quá bất ngờ ở trong nhà toán học tập Pháp Francois Viète. Định lí này gom tất cả chúng ta tính được những nghiệm của phương trình bậc tía bên dưới dạng bất đẳng thức vô cùng. Với công thức này, tất cả chúng ta hoàn toàn có thể xử lý những yếu tố phức tạp trong số nghành nghề như khoa học tập, tài chính hoặc chuyên môn với phỏng đúng đắn cao và nhanh gọn.
Định lý Vi-ét là gì và được dùng vô tình huống nào?
Định lý Vi-ét vô toán học tập là 1 trong những công thức tính những nghiệm của phương trình bậc tía. Định lý này được đặt điều theo dõi thương hiệu ở trong nhà toán học tập Pháp François Viète.
Công thức Vi-ét cho tới phương trình bậc tía với dạng ax^3 + bx^2 + cx + d = 0 là:
x1 + x2 + x3 = -b/a
x1x2 + x1x3 + x2x3 = c/a
x1x2x3 = -d/a
Trong ê, x1, x2, và x3 là tía nghiệm của phương trình bên trên.
Định lý Vi-ét được dùng vô tình huống đo lường và tính toán những nghiệm của phương trình bậc tía lúc không thể giải được bởi vì cách thức không giống. Nó cũng là 1 trong những trong mỗi dụng cụ cần thiết vô giải tích và đại số.
Bạn đang xem: Tìm hiểu định lý viet bậc 3 đơn giản nhất cho người mới bắt đầu
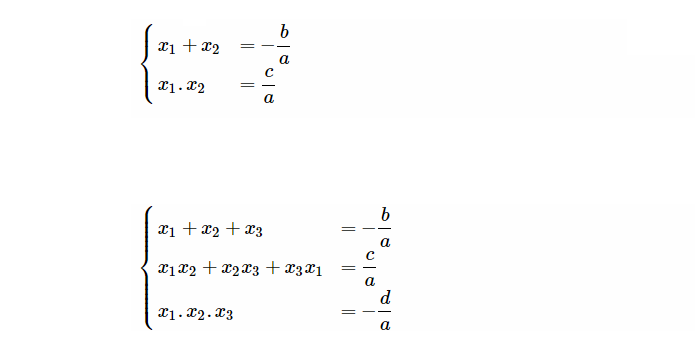

Công thức tính nghiệm của phương trình bậc 3 theo dõi lăm le lý Vi-ét?
Theo lăm le lý Vi-ét, công thức tính nghiệm của phương trình bậc 3 là:
- Cho phương trình ax^3 + bx^2 + cx + d = 0 (với a ≠ 0)
- Gọi t là số thực độc nhất thỏa mãn: t^2 = (3ac - b^2) / (3a^2)
- Khi ê, phương trình bậc tía trở thành: (x - (t + b / 3a))(x^2 + (2t + b / a)x + (t^2 + (b / a)t + c / a)) = 0
- Vậy, phương trình bậc 3 với 3 nghiệm là:
x1 = t + (b / 3a) + (u / 3a) (với u là √(3a^2t + 2bt + 3c) và với lốt \"+/-\" phù hợp)
x2 = t + (b / 3a) - (u / 6a) - (√3 / 6a)(t + (b / 3a) + (u / 3a) - (v / 3a))
x3 = t + (b / 3a) - (u / 6a) + (√3 / 6a)(t + (b / 3a) + (u / 3a) - (v / 3a))
Với công thức này, tất cả chúng ta hoàn toàn có thể tính được những nghiệm của phương trình bậc 3 theo dõi lăm le lý Vi-ét.
Tại sao chỉ mất tía nghiệm cho 1 phương trình bậc 3 theo dõi lăm le lý Vi-ét?
Theo lăm le lý Vi-ét, phương trình bậc 3 với tía nghiệm phân biệt. Như vậy vì thế công thức Vi-ét cho là tổng nhị nghiệm của phương trình là ngược so với rốn sót lại và tích tía nghiệm bởi vì thông số của độ quý hiếm bậc nhị của phương trình phân chia cho tới thông số của độ quý hiếm bậc tía. Vì vậy, nếu như tiếp tục biết nhị nghiệm của phương trình, tao hoàn toàn có thể dễ dàng và đơn giản đo lường và tính toán được nghiệm loại tía. Do ê, phương trình bậc 3 chỉ mất tía nghiệm phân biệt theo dõi lăm le lý Vi-ét.

Xem thêm:
Phương trình bậc 3 hoàn toàn có thể giải bởi vì cách thức nào là không giống ngoài lăm le lý Vi-ét?
Có thể giải phương trình bậc 3 bởi vì cách thức không giống ngoài lăm le lý Vi-ét là dùng cách thức group và cách thức đồng dư.
Phương pháp group là cách thức mò mẫm đi ra một fake thuyết về những nghiệm của phương trình, tiếp sau đó tạo thành những group nhằm giải từng group riêng lẻ. Phương pháp này đôi lúc hoàn toàn có thể giải phương trình bậc 3 một cơ hội giản dị và hiệu suất cao.
Phương pháp đồng dư dựa vào việc dùng đồng dư modulo nhằm giải phương trình. Phương pháp này hoàn toàn có thể giải được một trong những phương trình bậc 3 giản dị, tuy nhiên ko cần là cách thức khả dụng cho tới toàn bộ những loại phương trình bậc 3.
Tuy nhiên, lăm le lý Vi-ét là cách thức giải phương trình bậc 3 thông dụng và đúng đắn nhất, nên thông thường được dùng.
Có thể vận dụng lăm le lý Vi-ét cho những phương trình bậc cao hơn nữa không?
Có thể vận dụng lăm le lý Vi-ét cho những phương trình bậc cao hơn nữa tía, tuy nhiên phương pháp tính tiếp tục phức tạp rộng lớn và yên cầu kiến thức và kỹ năng cao hơn nữa về đại số và phép tắc tính đặc biệt quan trọng. Định lý Vi-ét chỉ vận dụng được cho những phương trình với dạng ax^n + bx^(n-1) + cx^(n-2) + ... + k = 0, với n là số vẹn toàn dương và a, b, c, ..., k là những hằng số. Tuy nhiên, Khi n tăng thêm, phương trình sẽ sở hữu được nghiệm phức, điều này thực hiện cho tới việc đo lường và tính toán trở thành phiền nhiễu và phức tạp rộng lớn.
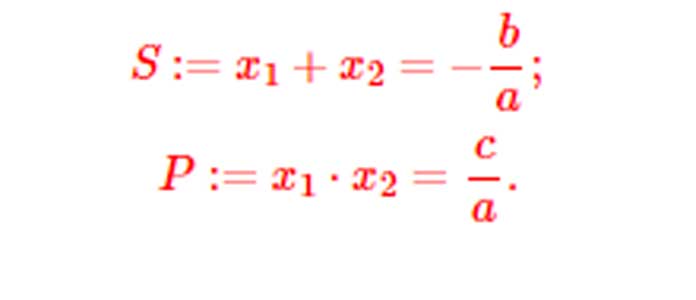
Xem thêm: Ứng dụng AI tạo ảnh anime gây sốt tại Việt Nam
_HOOK_
Phương pháp Cardano giải phương trình bậc tía tổng quát
Phương trình bậc tía là 1 trong những chủ thể cần thiết vô toán học tập và cũng là 1 trong những trong mỗi chủ thể khó khăn nhất. Nếu mình muốn xử lý phương trình bậc tía một cơ hội dễ dàng và đơn giản và nhanh gọn, hãy coi video clip của Cửa Hàng chúng tôi nhằm mò mẫm hiểu công việc xử lý phương trình bậc tía một cơ hội cụ thể và giản dị.
Ứng dụng Vi-et chứa chấp thông số m (nâng cao) - Phần 1
Vi-et chứa chấp thông số m là 1 trong những phần của đại số và được dùng rộng thoải mái vô toán học tập. Nếu mình muốn làm rõ rộng lớn về ghi chép chứa chấp thông số m và phương pháp vận dụng vô thực tiễn, hãy coi video clip của Cửa Hàng chúng tôi nhằm học tập công việc xử lý và những ví dụ tương quan cho tới ghi chép chứa chấp thông số m.