Bí quyết tính diện tích tam giác thường, vuông, cân, đều, đồng thời có bài tập thực hành.

Đặc biệt hóa công thức tính diện tích S tam giác Thường, Vuông, Cân, Đều và vận dụng vô bài xích tập luyện thực hành thực tế hiệu suất cao.

Khám phá huỷ phương pháp tính diện tích S tam giác vô hình vuông vắn, hình bình hành và học tập phương pháp tính diện tích S tam giác thông thường, vuông, cân nặng, đều trải qua ví dụ minh họa.

Bạn đang xem: Bí quyết tính diện tích tam giác thường, vuông, cân, đều, đồng thời có bài tập thực hành.

Với mẹo tính diện tích S tam giác, học viên và SV rất có thể nhanh gọn vận dụng vô bài học kinh nghiệm và triển khai xong việc làm một cơ hội thuận tiện.

Cách tính diện tích S tam giác, phương pháp tính diện tích S tam giác vuông, cân nặng, đều

Mục Lục bài xích viết: 1. Khám phá huỷ định nghĩa tam giác. 2. Phương pháp tính diện tích S tam giác. 3. Bế Tắc quyết tính diện tích S tam giác nâng lên. 4. Lưu ý. 5. Bài tập luyện.

Tổng phù hợp phương pháp tính diện tích S Tam Giác: Thường, Vuông, Cân, Đều

1. Tam giác là gì? Khám phá huỷ những tình huống đặc trưng của tam giác.

Để giải bài xích tập luyện về diện tích S tam giác, trước không còn, xác lập loại tam giác và vận dụng công thức đúng đắn nhất. Có 7 dạng tam giác phổ cập như sau:

Xem thêm thắt cụ thể bên trên Wikipedia: Tìm hiểu về tam giác.

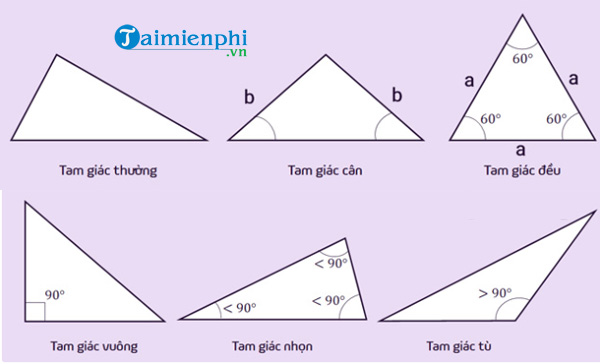
Hình hình ảnh những loại tam giác phổ cập.

Để hiểu sâu sắc về đàng cao vô tam giác, nhất là tam giác đều, tam giác vuông, và tam giác cân nặng, phát âm thêm:

2. Cách tính diện tích S tam giác

Để minh họa rõ ràng rộng lớn, Mytour tiếp tục chỉ dẫn phương pháp tính diện tích S tam giác kể từ tam giác thông thường cho tới những tình huống đặc trưng như tam giác vuông, cân nặng, đều,...

* Cách tính diện tích S tam giác thường

- Diễn giải: Diện tích tam giác thông thường được xem bằng phương pháp nhân độ cao với phỏng lâu năm lòng, tiếp sau đó phân chia mang đến 2. Nói cách tiếp, diện tích S tam giác thông thường vị một nửa tích của độ cao và chiều lâu năm cạnh lòng của tam giác.
- Công thức tính diện tích S tam giác thường

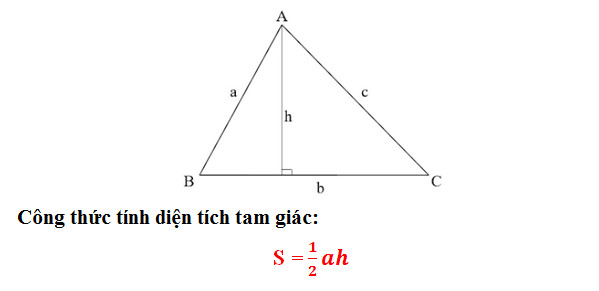
Trong đó:

+ a: Chiều lâu năm lòng tam giác (đáy là 1 trong vô 3 cạnh của tam giác tùy từng quy đặt điều của những người tính)
+ h: Chiều cao của tam giác, ứng với phần lòng chiếu lên (chiều cao tam giác vị đoạn trực tiếp hạ kể từ đỉnh xuống lòng, bên cạnh đó vuông góc với lòng của một tam giác).

- Nếu vẫn sở hữu diện tích S tam giác, chúng ta cũng có thể tìm hiểu đàng cao hoặc cạnh tam giác với công thức như sau:
+ Đường cao H= (Sx2)/ a
+ Công thức tính cạnh tam giác ứng với chiều cao: a= (Sx2)/ h
- Ví dụ: Cho một hình tam giác ABC, vô cơ sở hữu độ cao nối kể từ đỉnh Hình ảnh xuống lòng BC vị 3, chiều lâu năm lòng BC vị 6. Tính diện tích S tam giác thông thường ABC? (Đơn vị tính: cm)

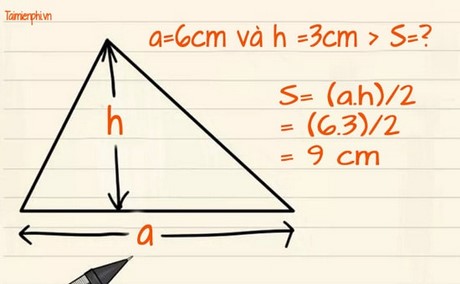
Đáp án: Gọi a =6 và h=3.
Suy ra S = (a x h)/ 2 = (6x3)/2 hoặc một nửa x (6x3) = 9 cm
* Chú ý: Trường phù hợp ko mang đến cạnh lòng hoặc độ cao, tuy nhiên mang đến trước diện tích S và cạnh sót lại, chúng ta hãy vận dụng công thức suy rời khỏi phía trên nhằm đo lường.

* Cách tính diện tích S tam giác vuông

- Diễn giải: Cách tính diện tích S tam giác vuông tương tự động với phương pháp tính diện tích S tam giác thông thường, này đó là vị một nửa tích của độ cao với chiều lâu năm lòng. Mặc cho dù vậy hình tam giác vuông tiếp tục khác lạ rộng lớn đối với tam giác thông thường tự thể hiện tại rõ ràng độ cao và chiều lâu năm cạnh lòng, và chúng ta ko cần thiết vẽ thêm thắt nhằm tính độ cao tam giác.
- Công thức tính diện tích S tam giác vuông: S = (a x h)/ 2
+ a: Chiều lâu năm lòng tam giác vuông (đáy là 1 trong vô 3 cạnh của tam giác và vuông góc với cùng một cạnh còn lại)
+ h: Chiều cao của tam giác, ứng với phần lòng chiếu lên (chiều cao tam giác vị đoạn trực tiếp hạ kể từ đỉnh xuống lòng, bên cạnh đó vuông góc với lòng của một tam giác).
Từ cơ, suy ra sức thức độ cao, cạnh ứng là: h=(Sx2)/ a hoặc a= (Sx2)/ h
- Ví dụ: Có một hình tam giác vuông ABC, vuông góc nhau bên trên điểm B, chiều lâu năm cạnh lòng BC là 5 centimet, độ cao là 2 centimet. Hỏi diện tích S của hình tam giác vuông ABC vị bao nhiêu? Đơn vị tính: centimet.

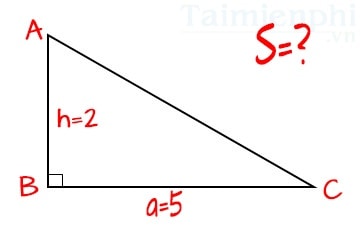
Đáp án: Gọi a =5 và h=2.
Suy ra S = (a x h)/ 2 = (5x2)/2 hoặc một nửa x (5x2) = 5 cm
Tương tự động nếu như tài liệu căn vặn ngược về kiểu cách tính chiều lâu năm cạnh lòng hoặc độ cao, những chúng ta cũng có thể dùng công thức suy rời khỏi phía trên.

* Cách tính diện tích S tam giác cân

Tam giác cân nặng là tam giác vô cơ sở hữu nhị cạnh mặt mày và nhị góc cân nhau. Cách tính diện tích S tam giác cân nặng tương tự động như phương pháp tính tam giác thông thường, chỉ việc chúng ta biết độ cao tam giác và cạnh lòng.
- Diễn giải: Diện tích tam giác thăng bằng Tích của độ cao nối kể từ đỉnh tam giác cho tới cạnh lòng tam giác, tiếp sau đó phân chia mang đến 2.
- Công thức tính diện tích S tam giác cân: S = (a x h)/ 2
+ a: Chiều lâu năm lòng tam giác cân nặng (đáy là 1 trong vô 3 cạnh của tam giác)
+ h: Chiều cao của tam giác (chiều cao tam giác vị đoạn trực tiếp hạ kể từ đỉnh xuống đáy).
- Ví dụ: Cho một tam giác cân nặng ABC sở hữu độ cao nối kể từ đỉnh A xuống lòng BC vị 7 centimet, chiều lâu năm lòng là 6 centimet. Hỏi diện tích S của tam giác cân nặng ABC vị từng nào.

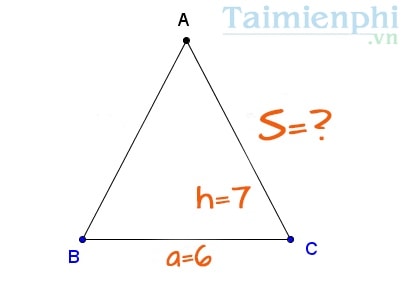
Đáp án: Gọi a =6 và h=7.
Suy ra S = (a x h)/ 2 = (6x7)/2 hoặc một nửa x (6x7) = 21 cm

* Công thức tính diện tích S tam giác vuông cân

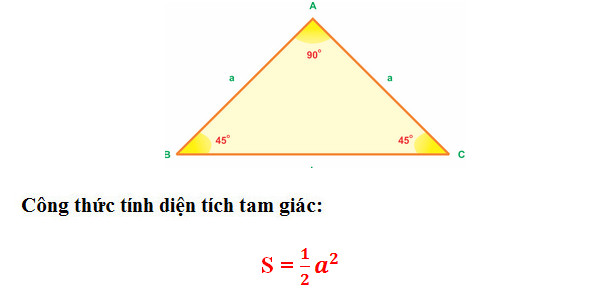
Ví dụ: Cho tam giác ABC vuông cân nặng bên trên A, sở hữu AB = AC = 6cm. Tính diện tích S tam giác ABC.
Giải: Do cạnh AB = AC = a = 6cm
Xét tam giác ABC vuông cân nặng bên trên A, tao có:
S = (a²) : 2 = 36 : 2 = 13 cm²

* Công thức tính diện tích S tam giác đều
Tam giác đều là tam giác sở hữu 3 cạnh cân nhau và từng góc vô tam giác đều sở hữu góc vị 60 phỏng, và bất kể tam giác này sở hữu tía góc cân nhau cũng rất được xem là một tam giác đều.
- Công thức diện tích S tam giác đều:  S = a² X (√3)/4

Trong đó:
+ a: chiều lâu năm một cạnh ngẫu nhiên vô tam giác đều.
- Ví dụ: Có một tam giác đều ABC với chiều lâu năm những cạnh cân nhau là 9 centimet, biết những góc của tam giác này đều vị 60 phỏng. Hỏi diện tích S tam giác đều ABC vị bao nhiêu?

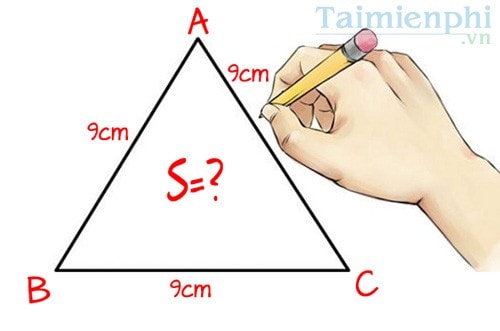
Đáp án: Do từng cạnh AB = AC = BC = 9 nên tao sở hữu chiều lâu năm cạnh a = 9.

Thay vô công thức diện tích S tam giác đều tao có: S = a² x (√3)/4 = S = 9² x (√3)/4  = 81 x  (√3)/4 = 81 x  (1,732/4) = 35,07 cm²

3. Các phương pháp tính diện tích S tam giác nâng cao

Ngoài những phương pháp tính diện tích S tam giác phía trên, thực tiễn, toán học tập còn dùng những cách thức tính diện tích S tam giác vị công thức Heron, tính diện tích S tam giác trải qua góc và nồng độ giác. Cụ thể:

* Diện tích tam giác lúc biết 1 góc

Xem thêm: Vé máy bay giá rẻ đi Thanh Hóa (THD) với giá chỉ từ 1.402.282₫ | Trip.com

Diện tích tam giác theo dõi Sin là:

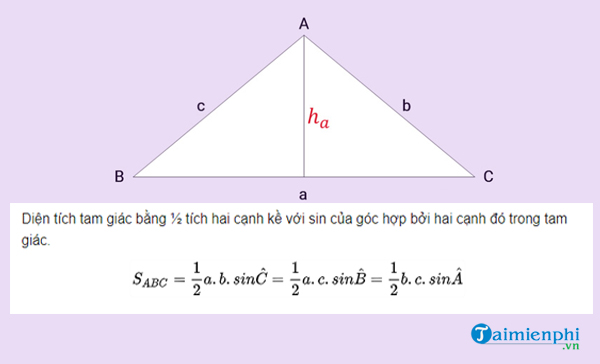
* Công thức tính diện tích S tam giác theo dõi công thức Heron
Diện tích tam giác lúc biết 3 cạnh: 

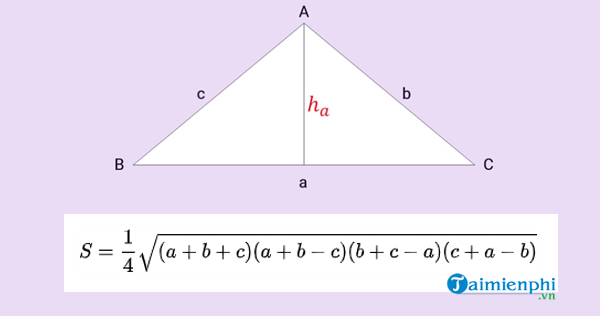
* Cách tính diện tích S tam giác phanh rộng

Lưu ý: Khi dùng công thức này, cần thiết minh chứng trước. 

Công thức 1:

Trong đó:

- a, b, c: Độ lâu năm những cạnh của tam giác

Công thức 2: 

Diện tích tam giác rất có thể tính vị công thức sau: 

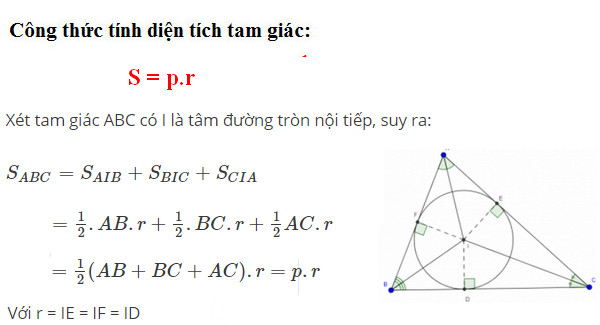
Trong đó:

- p: Nửa chu vi tam giác

Tùy nằm trong vào cụ thể từng loại tam giác và Lever khối lớp, sẽ có được những công thức tính diện tích S không giống nhau. Các em học viên lớp 5, lớp 8 thông thường vận dụng công thức cơ phiên bản và giản dị và đơn giản. Đến lớp 10 trở lên trên, khi vẫn nắm rõ kiến thức và kỹ năng về lượng giác, đàng tròn xoe nội, nước ngoài tiếp, rất có thể vận dụng những công thức phức tạp rộng lớn.

4. Một số cảnh báo khi tính diện tích S tam giác

- Trong quy trình đo lường, hãy đáp ứng những đơn vị chức năng giám sát và đo lường như nhau.
- Diện tích được giám sát và đo lường theo dõi đơn vị chức năng nón 2, ví như m², cm²,...
- Cần lưu ý rằng độ cao ko cần khi nào thì cũng nằm trong tam giác. Trong tình huống này, cần thiết vẽ thêm 1 độ cao và cạnh lòng bổ sung cập nhật. Quan trọng nhất, khi tính diện tích S tam giác, độ cao cần ứng với cạnh lòng điểm nó chiếu xuống.

5. Bài thói quen diện tích S tam giác

Giải bài xích 1 Trang 88 SGK Toán 5:

Tính diện tích S hình tam giác với:

a) Độ lâu năm lòng là 8cm và độ cao là 6cm.

b) Độ lâu năm lòng là 2,3dm và độ cao là một,2dm.

Hướng dẫn giải:

a, Diện tích của hình tam giác là một nửa x 8 x 6 = 24 (cm²)

b, Diện tích hình tam giác là một nửa x 2,3 x 1,2 = 1,38  (dm²)

Ví dụ 1: Một hình tam giác sở hữu lòng 15 centimet và độ cao 2,4cm. Tính diện tích S hình tam giác đó?
Hướng dẫn giải:
Diện tích hình tam giác là:
15 x 2,4 : 2 = 18 (cm²)
Đáp số: 18cm²

Ví dụ 2: Một hình tam giác sở hữu lòng 12cm và độ cao 25mm. Tính diện tích S hình tam giác đó?

Hướng dẫn giải

Đổi: 25mm = 2,5 cm

Diện tích của hình tam giác là:

12 x 2,5 : 2 = 15 (cm²)

Đáp số: 15cm²

=> Các em rất có thể xem thêm thêm thắt các bài toán về hình tam giác lớp 5 cơ phiên bản và nâng lên nhằm hiểu rộng lớn về kiểu cách giải, thực hiện vấn đề này dễ dàng dàng/ 

""""---HẾT""""---

Xem thêm: Thì quá khứ đơn (Simple Past) – Công thức, cách dùng, dấu hiệu và bài tập

Hiện ni, có tương đối nhiều khí cụ tương hỗ đo lường, nhất là những em học viên, như FxCalc, DubCen, SpeQ Mathematics, Calculatormatik, Magiccalc, vận chuyển CocCoc giải toán,… đa phần người thông thường đo lường vị Fxcalc hoặc dùng CocCoc giải toán vì như thế tính tiện nghi và hiệu suất cao.

Các em vẫn tìm hiểu hiểu về tam giác và phương pháp vẽ nó. Bây giờ, hãy nằm trong tìm hiểu công thức tính chu vi tam giác!