Bài viết lách chỉ dẫn cách thức phần mềm tích phân nhằm tính thể tích khối tròn xoay khi xoay quanh Ox hình bằng số lượng giới hạn bởi vì một đàng cong và trục hoành.
I. KIẾN THỨC CẦN NHỚ
1. Cho hình bằng số lượng giới hạn bởi vì thiết bị thị hàm số $y = f(x)$ liên tiếp bên trên đoạn $[a;b]$, trục $Ox$ và hai tuyến đường trực tiếp $x= a$, $x=b$ xoay quanh $Ox$ tớ được khối tròn trặn xoay hoàn toàn có thể tích là: $V = \pi \int_a^b {{f^2}} (x)dx.$
Bạn đang xem: Thể tích khối tròn xoay khi quay quanh Ox hình phẳng giới hạn bởi một đường cong và trục hoành - TOANMATH.com

2. Cho hình bằng số lượng giới hạn bởi vì thiết bị thị hàm số $y = f(x)$ và trục hoành xoay quanh $Ox$ tớ được khối tròn trặn xoay hoàn toàn có thể tích là $V = \pi \int_\alpha ^\beta {{f^2}} (x)dx$, nhập cơ $\alpha $, $\beta $ theo lần lượt là nghiệm nhỏ nhất và lớn số 1 của phương trình $f(x) = 0.$
II. BÀI TẬP TRẮC NGHIỆM MINH HỌA
Ví dụ 1: Thể tích khối tròn trặn xoay tạo ra trở nên khi cho tới hình bằng số lượng giới hạn bởi vì thiết bị thị hàm số $y = f(x)$ liên tiếp bên trên đoạn $[a;b]$, trục $Ox$ và hai tuyến đường trực tiếp $x= a$, $x = b$ xoay quanh $Ox$ được xem bởi vì công thức này sau đây?
A. $V = \int_a^b {{f^2}} (x)dx.$
B. $V = \pi \int_a^b f (x)dx.$
C. $V = \int_a^b | f(x)|dx.$
D. $V = \pi \int_a^b {{f^2}} (x)dx.$
Lời giải:
Theo lý thuyết tớ với $V = \pi \int_a^b {{f^2}} (x)dx.$
Chọn đáp án D.
Ví dụ 2: Cho hàm số $y=f(x)$ liên tiếp bên trên đoạn $[a;b].$ Hình bằng số lượng giới hạn bởi vì những đàng $y = f(x)$, $y=0$, $x= a$, $x=b$ xoay quanh trục $Ox$ hoàn toàn có thể tích là ${V_1}.$ Hình bằng số lượng giới hạn bởi vì những đàng $y = \sqrt {2018} f(x)$, $y=0$, $x= a$, $x=b$ xoay quanh trục $Ox$ hoàn toàn có thể tích là ${V_2}.$ Khẳng quyết định này sau đấy là đúng?
A. ${V_1} = 2018{V_2}.$
B. ${V_2} = 2018{V_1}.$
C. ${V_1} = \sqrt {2018} {V_2}.$
D. ${V_2} = \sqrt {2018} {V_1}.$
Lời giải:
${V_1} = \pi \int_a^b {{f^2}} (x)dx.$
${V_2} = \pi \int_a^b {{{[\sqrt {2018} f(x)]}^2}dx} $ $ = 2018\pi \int_a^b {{f^2}} (x)dx.$
${V_2} = 2018{V_1}.$
Chọn đáp án B.
Ví dụ 3: Cho hình bằng $H$ số lượng giới hạn bởi vì đàng cong $y = \sqrt {3{x^2} + 2} $, trục hoành và những đường thẳng liền mạch $x=0$, $x=2.$ Khối tròn trặn xoay tạo ra trở nên khi xoay $H$ xung quanh trục hoành hoàn toàn có thể tích bằng:
A. $8\pi .$
B. $10\pi .$
C. $12\pi .$
D. $14\pi .$
Lời giải:
$V = \pi \int_0^2 {\left( {3{x^2} + 2} \right)dx} $ $ = \left. {\pi \left( {{x^3} + 2x} \right)} \right|_0^2$ $ = 12\pi .$
Chọn đáp án C.
Ví dụ 4: Cho hình bằng $H$ số lượng giới hạn bởi vì những đàng $y=2x+1$, $y=0$, $x=0$, $x=1.$ Khối tròn trặn xoay tạo ra trở nên khi xoay $H$ xung quanh trục hoành hoàn toàn có thể tích bằng:
A. ${2\pi .}$
B. ${3\pi .}$
C. ${\frac{9}{2}.}$
D. ${\frac{{13\pi }}{3}}.$
Lời giải:
$V = \pi \int_0^1 {{{(2x + 1)}^2}} dx$ $ = \left. {\pi \frac{{{{(2x + 1)}^3}}}{6}} \right|_0^1$ $ = \frac{{13\pi }}{3}.$
Chọn đáp án D.
Ví dụ 5: Cho hình bằng $H$ số lượng giới hạn bởi vì những đàng $y = x – {x^2}$ và trục hoành. Khối tròn trặn xoay tạo ra trở nên khi xoay $H$ xung quanh trục hoành hoàn toàn có thể tích bằng:
A. $\frac{1}{{30}}.$
B. $\frac{\pi }{{30}}.$
C. $\frac{1}{6}.$
D. $\frac{\pi }{6}.$
Lời giải:
Tìm hoành chừng gửi gắm điểm: $x – {x^2} = 0$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 0}\\
{x = 1}
\end{array}} \right..$
Thể tích: $V = \pi \int_0^1 {{{\left( {x – {x^2}} \right)}^2}} dx = \frac{\pi }{{30}}.$
Chọn đáp án B.
Ví dụ 6: Cho hình bằng $H$ số lượng giới hạn bởi vì những đàng $y = \sqrt {1 – {x^2}} $ và trục hoành. Khối tròn trặn xoay tạo ra trở nên khi xoay $H$ xung quanh trục hoành hoàn toàn có thể tích bởi vì $\frac{a}{b}\pi $ với $a$, $b$ là những số nguyên vẹn dương và $\frac{a}{b}$ là phân số tối giản. Tính $T = 2a +b.$
A. $T=-11.$
B. $T=-10.$
C. $T =10.$
D. $T=11.$
Lời giải:
Tìm hoành chừng gửi gắm điểm: $\sqrt {1 – {x^2}} = 0$ $ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = – 1}\\
{x = 1}
\end{array}} \right..$
Thể tích: $V = \pi \int_{ – 1}^1 {\left( {1 – {x^2}} \right)dx} = \frac{{4\pi }}{3}$ $ \Rightarrow a = 4$, $b = 3$ $ \Rightarrow T = 2a + b = 11.$
Chọn đáp án D.
Ví dụ 7: Cho hình bằng $H$ số lượng giới hạn bởi vì những đàng $y = \sqrt {\sin x} $, $y = 0$, $x = 0$, $x = \frac{{3\pi }}{4}.$ Khối tròn trặn xoay tạo ra trở nên khi xoay $H$ xung quanh trục hoành hoàn toàn có thể tích $V$ bởi vì bao nhiêu?
A. $V = \frac{{\pi \sqrt 2 }}{2}.$
B. $V = \pi \left( {\frac{{\sqrt 2 }}{2} – 1} \right).$
C. $V = \pi \left( {\frac{{\sqrt 2 }}{2} + 1} \right).$
D. $V = \frac{{\sqrt 2 }}{2} + 1.$
Lời giải:
$V = \pi \int_0^{\frac{{3\pi }}{4}} {\sin xdx} $ $ = – \left. {\pi \cos x} \right|_0^{\frac{{3\pi }}{4}}$ $ = \pi \left( {\frac{{\sqrt 2 }}{2} + 1} \right).$
Chọn đáp án C.
Ví dụ 8: Cho hình bằng $H$ số lượng giới hạn bởi vì những đàng $y = \cos x$, $y = 0$, $x = 0$, $x = \frac{\pi }{2}.$ Khối tròn trặn xoay tạo ra trở nên khi xoay $H$ xung quanh trục hoành hoàn toàn có thể tích $V$ bởi vì bao nhiêu?
A. $V = \frac{\pi }{4}.$
B. $V = \frac{{{\pi ^2}}}{4}.$
C. $V = \frac{\pi }{2}\left( {\frac{\pi }{2} – 1} \right).$
D. $V = \frac{\pi }{2}\left( {\frac{\pi }{2} + 1} \right).$
Lời giải:
$V = \pi \int_0^{\frac{\pi }{2}} {{{\cos }^2}} xdx$ $ = \frac{\pi }{2}\int_0^{\frac{\pi }{2}} {(1 + \cos 2x)dx} $ $ = \left. {\frac{\pi }{2}\left( {x + \frac{1}{2}\sin 2x} \right)} \right|_0^{\frac{\pi }{2}}$ $ = \frac{{{\pi ^2}}}{4}.$
Chọn đáp án B.
Ví dụ 9: Cho hình bằng $H$ số lượng giới hạn bởi vì những đàng $y = \sin x$, $y = 0$, $x = 0$, $x = \frac{\pi }{4}.$ Khối tròn trặn xoay tạo ra trở nên khi xoay $H$ xung quanh trục hoành hoàn toàn có thể tích $V$ bởi vì bao nhiêu?
A. $V = \frac{1}{2}\left( {\frac{\pi }{4} + \frac{{\sqrt 2 }}{2}} \right).$
B. $V = \frac{1}{2}\left( {\frac{\pi }{4} – \frac{{\sqrt 2 }}{2}} \right).$
C. $V = \frac{\pi }{2}\left( {\frac{\pi }{4} – \frac{1}{2}} \right).$
D. $V = \frac{\pi }{2}\left( {\frac{\pi }{4} + \frac{1}{2}} \right).$
Lời giải:
$V = \pi \int_0^{\frac{\pi }{4}} {{{\sin }^2}} xdx$ $ = \frac{\pi }{2}\int_0^{\frac{\pi }{4}} {(1 – \cos 2x)dx} $ $ = \left. {\frac{\pi }{2}\left( {x – \frac{1}{2}\sin 2x} \right)} \right|_0^{\frac{\pi }{4}}$ $ = \frac{\pi }{2}\left( {\frac{\pi }{4} – \frac{1}{2}} \right).$
Chọn đáp án C.
Ví dụ 10: Cho hình bằng $H$ số lượng giới hạn bởi vì những đàng $y = \tan x$, $y = 0$, $x = 0$, $x = \frac{\pi }{4}.$ Khối tròn trặn xoay tạo ra trở nên khi xoay $H$ xung quanh trục hoành hoàn toàn có thể tích $V$ bởi vì bao nhiêu?
A. $V = 1 – \frac{\pi }{4}.$
B. $V = \pi \left( {1 – \frac{\pi }{4}} \right).$
C. $V = \frac{\pi }{3}.$
D. $V = 2\pi .$
Lời giải:
$V = \pi \int_0^{\frac{\pi }{4}} {{{\tan }^2}} xdx$ $ = \pi \int_0^{\frac{\pi }{4}} {\left( {\frac{1}{{{{\cos }^2}x}} – 1} \right)dx} $ $ = \left. {\pi (\tan x – x)} \right|_0^{\frac{\pi }{4}}$ $ = \pi \left( {1 – \frac{\pi }{4}} \right).$
Chọn đáp án B.
Ví dụ 11: Cho hình bằng $H$ số lượng giới hạn bởi vì những đàng $y = \sin x + \cos x$, $y = 0$, $x = 0$, $x = \frac{\pi }{2}.$ Khối tròn trặn xoay tạo ra trở nên khi xoay $H$ xung quanh trục hoành hoàn toàn có thể tích $V$ bởi vì bao nhiêu?
A. $V = \pi \left( {\frac{1}{2} + \frac{\pi }{4}} \right).$
B. $V = \pi \left( {1 + \frac{\pi }{4}} \right).$
C. $V = \pi \left( {\frac{\pi }{2} + 1} \right).$
D. $V = \frac{{\pi (\pi + 1)}}{2}.$
Lời giải:
$V = \pi \int_0^{\frac{\pi }{2}} {{{(\sin x + \cos x)}^2}} dx$ $ = \pi \int_0^{\frac{\pi }{2}} {(1 + \sin 2x)dx} $ $ = \left. {\pi \left( {x – \frac{1}{2}\cos 2x} \right)} \right|_0^{\frac{\pi }{2}}$ $ = \pi \left( {\frac{\pi }{2} + 1} \right).$
Chọn đáp án C.
Ví dụ 12: Cho hình bằng $H$ số lượng giới hạn bởi vì những đàng $y = \sqrt {2 + \sin x – \cos x} $, $y = 0$, $x = 0$, $x = \frac{\pi }{2}.$ Khối tròn trặn xoay tạo ra trở nên khi xoay $H$ xung quanh trục hoành hoàn toàn có thể tích $V$ bởi vì bao nhiêu?
A. $V = \frac{\pi }{2}.$
B. $V = \pi .$
C. $V = \frac{{{\pi ^2}}}{2}.$
D. $V = {\pi ^2}.$
Lời giải:
$V = \pi \int_0^{\frac{\pi }{2}} {(2 + \sin x – \cos x)dx} $ $ = \left. {\pi (2x – \cos x – \sin x)} \right|_0^{\frac{\pi }{2}}$ $ = {\pi ^2}.$
Chọn đáp án D.
Ví dụ 13: Cho hình bằng $H$ số lượng giới hạn bởi vì những đàng $y = \sqrt {1 + \cos x} $, $y = 0$, $x = 0$, $x = \frac{\pi }{6}.$ Khối tròn trặn xoay tạo ra trở nên khi xoay $H$ xung quanh trục hoành hoàn toàn có thể tích bởi vì $\frac{{{\pi ^2}}}{a} + \frac{\pi }{b}$ với $a$, $b$ là những số nguyên vẹn. Khẳng quyết định này sau đấy là đúng?
A. $a+2b = 10.$
B. $a<b.$
C. $a>2b.$
D. $2a+b=10.$
Lời giải:
$V = \pi \int_0^{\frac{\pi }{6}} {(1 + \cos x)dx} $ $ = \left. {\pi (x + \sin x)} \right|_0^{\frac{\pi }{6}}$ $ = \pi \left( {\frac{\pi }{6} + \frac{1}{2}} \right)$ $ = \frac{{{\pi ^2}}}{6} + \frac{\pi }{2}$ $ \Rightarrow a = 6$, $b = 2.$
$ \Rightarrow a + 2b = 10.$
Chọn đáp án A.
Ví dụ 14: Cho hình bằng $D$ số lượng giới hạn bởi vì đàng cong $y = \sqrt {2 + \sin x} $, trục hoành và những đường thẳng liền mạch $x = 0$, $x = \pi .$ Khối tròn trặn xoay tạo ra trở nên khi xoay $D$ xung quanh trục hoành hoàn toàn có thể tích $V$ bởi vì bao nhiêu?
A. $V = 2{\pi ^2}.$
B. $V = 2\pi (\pi + 1).$
C. $V = 2\pi .$
D. $V = 2(\pi + 1).$
Lời giải:
$V = \pi \int_0^\pi {{{(\sqrt {2 + \sin x} )}^2}} dx$ $ = \pi \int_0^\pi {(2 + \sin x)dx} $ $ = \left. {\pi (2x – \cos x)} \right|_0^\pi $ $ = 2\pi (\pi + 1).$
Chọn đáp án B.
Ví dụ 15: Cho hình bằng $D$ số lượng giới hạn bởi vì đàng cong $y = 1 + 2\sin x$, trục hoành và những đường thẳng liền mạch $x = 0$, $x = \frac{\pi }{2}.$ Khối tròn trặn xoay tạo ra trở nên khi xoay $D$ xung quanh trục hoành hoàn toàn có thể tích bởi vì $\frac{a}{b}{\pi ^2} + c\pi $ với $a$, $b$, $c$ là những số nguyên vẹn dương, $\frac{a}{b}$ là phân số tối giản. Tính $T = a + {b^2} + c.$
A. $T=11.$
B. $T=15.$
C. $T = 21.$
D. $T=25.$
Lời giải:
$V = \pi \int_0^{\frac{\pi }{2}} {{{(1 + 2\sin x)}^2}} dx$ $ = \pi \int_0^{\frac{\pi }{2}} {\left( {1 + 4\sin x + 4{{\sin }^2}x} \right)dx} .$
$ = \pi \int_0^{\frac{\pi }{2}} {(3 + 4\sin x – 2\cos 2x)dx} $ $ = \left. {\pi (3x – 4\cos x – \sin 2x)} \right|_0^{\frac{\pi }{2}}$ $ = \frac{{3{\pi ^2}}}{2} + 4\pi .$
$ \Rightarrow a = 3$, $b = 2$, $c = 4$ $ \Rightarrow T = a + {b^2} + c = 11.$
Chọn đáp án A.
Ví dụ 16: Cho hình bằng $D$ số lượng giới hạn bởi vì đàng cong $y = \sqrt {{{\sin }^4}x + {{\cos }^4}x} $, trục hoành và những đường thẳng liền mạch $x = 0$, $x = \frac{\pi }{2}.$ Khối tròn trặn xoay tạo ra trở nên khi xoay $D$ xung quanh trục hoành hoàn toàn có thể tích bởi vì $\frac{a}{b}{\pi ^2}$ với $a$, $b$ là những số nguyên vẹn dương, $\frac{a}{b}$ là phân số tối giản. Tính $T= 2a + 3b.$
A. $T = 25.$
B. $T= 30.$
C. $T = 35.$
D. $T = 40.$
Lời giải:
$V = \pi \int_0^{\frac{\pi }{2}} {\left( {{{\sin }^4}x + {{\cos }^4}x} \right)dx} $ $ = \pi \int_0^{\frac{\pi }{2}} {\left( {\frac{3}{4} + \frac{1}{4}\cos 2x} \right)dx} .$
$ = \left. {\pi \left( {\frac{{3x}}{4} + \frac{1}{8}\sin 2x} \right)} \right|_0^{\frac{\pi }{2}}$ $ = \frac{{3{\pi ^2}}}{8}.$
$ \Rightarrow a = 3$, $b = 8$ $ \Rightarrow T = 2a + 3b = 30.$
Chọn đáp án B.
Ví dụ 17: Cho hình bằng $D$ số lượng giới hạn bởi vì đàng cong $y = \sqrt {x\cos x} $, trục hoành và những đường thẳng liền mạch $x = 0$, $x = \frac{\pi }{2}.$ Khối tròn trặn xoay tạo ra trở nên khi xoay $D$ xung quanh trục hoành hoàn toàn có thể tích bởi vì $\frac{{{\pi ^2}}}{a} + b\pi $ với $a$, $b$ là những số nguyên vẹn. Tính $T = a – b + ab.$
A. $T=1.$
B. $T = 2.$
C. $T=3.$
D. $T=4.$
Lời giải:
$V = \pi \int_0^{\frac{\pi }{2}} x \cos xdx.$

Xem thêm: Ăn ngon với 9 quán lòng nướng Hà Nội chuẩn vị, bao sạch
$V = \left. {\pi (x\sin x + \cos x)} \right|_0^{\frac{\pi }{2}}$ $ = \frac{{{\pi ^2}}}{2} – \pi $ $ \Rightarrow a = 2$, $b = – 1$ $ \Rightarrow T = a – b + ab = 1.$
Chọn đáp án A.
Ví dụ 18: Cho hình bằng $D$ số lượng giới hạn bởi vì đàng cong $y = \sqrt {x(2 – \sin x)} $, trục hoành và những đường thẳng liền mạch $x = \frac{\pi }{2}.$ Khối tròn trặn xoay tạo ra trở nên khi xoay $D$ xung quanh trục hoành hoàn toàn có thể tích bởi vì $\pi \left( {\frac{{{\pi ^2}}}{a} – b} \right)$ với $a$, $b$ là những số nguyên vẹn. Tính $T = {a^2} + {b^2} – a.$
A. $T = 13.$
B. $T=16.$
D. $T = 21.$
C. $T = 18.$
Lời giải:
Tìm hoành chừng gửi gắm điểm: $\sqrt {x(2 – \sin x)} = 0$ $ \Leftrightarrow x = 0.$
Thể tích: $V = \pi \int_0^{\frac{\pi }{2}} x (2 – \sin x)dx.$

$V = \left. {\pi \left[ {x(2x + \cos x) – \left( {{x^2} + \sin x} \right)} \right]} \right|_0^{\frac{\pi }{2}}$ $ = \pi \left( {\frac{{{\pi ^2}}}{4} – 1} \right)$ $ \Rightarrow a = 4$, $b = 1.$
$ \Rightarrow T = {a^2} + {b^2} – a = 13.$
Chọn đáp án A.
Ví dụ 19: Cho hình bằng $D$ số lượng giới hạn bởi vì đàng cong $y = {e^x}$, trục hoành và những đường thẳng liền mạch $x=0$, $x=1.$ Khối tròn trặn xoay tạo ra trở nên khi xoay $D$ xung quanh trục hoành hoàn toàn có thể tích $V$ bởi vì bao nhiêu?
A. $V = \frac{{\pi {e^2}}}{2}.$
B. $V = \frac{{\pi \left( {{e^2} + 1} \right)}}{2}.$
C. $V = \frac{{{e^2} – 1}}{2}.$
D. $V = \frac{{\pi \left( {{e^2} – 1} \right)}}{2}.$
Lời giải:
$V = \pi \int_0^1 {{e^{2x}}} dx$ $ = \left. {\frac{\pi }{2}{e^{2x}}} \right|_0^1 = \frac{{\pi \left( {{e^2} – 1} \right)}}{2}.$
Chọn đáp án D.
Ví dụ 20: Cho hình bằng $D$ số lượng giới hạn bởi vì đàng cong $y = 2 + {e^x}$, trục hoành và những đường thẳng liền mạch $x=0$, $x=1.$ Khối tròn trặn xoay tạo ra trở nên khi xoay $D$ xung quanh trục hoành hoàn toàn có thể tích bởi vì $\pi \left( {\frac{{{e^2}}}{a} + be + \frac{1}{c}} \right)$ với $a$, $b$, $c$ là những số nguyên vẹn. Tính $T=a+2b+3c.$
A. $T=4.$
B. $T=6.$
C. $T=14.$
D. $T =16.$
Lời giải:
$V = \pi \int_0^1 {{{\left( {2 + {e^x}} \right)}^2}} dx$ $ = \pi \int_0^1 {\left( {4 + 4{e^x} + {e^{2x}}} \right)dx} .$
$ = \left. {\pi \left( {4x + 4{e^x} + \frac{1}{2}{e^{2x}}} \right)} \right|_0^1$ $ = \pi \left( {\frac{{{e^2}}}{2} + 4e – \frac{1}{2}} \right).$
$ \Rightarrow a = 2$, $b = 4$, $c = – 2$ $ \Rightarrow T = a + 2b + 3c = 4.$
Chọn đáp án A.
Ví dụ 21: Cho hình bằng $D$ số lượng giới hạn bởi vì đàng cong $y = \sqrt {4x + {e^x}} $, trục hoành và những đường thẳng liền mạch $x=0$, $x=1.$ Khối tròn trặn xoay tạo ra trở nên khi xoay $D$ xung quanh trục hoành hoàn toàn có thể tích bởi vì $\pi (a + be)$ với $a$, $b$ là những số nguyên vẹn. Tính $T = a + 5b + {\log _{2018}}a.$
A. $T=4.$
B. $T=6.$
C. $T=7.$
D. $T=9.$
Lời giải:
$V = \pi \int_0^1 {\left( {4x + {e^x}} \right)dx} $ $ = \left. {\pi \left( {2{x^2} + {e^x}} \right)} \right|_0^1$ $ = \pi (1 + e)$ $ \Rightarrow a = 1$, $b = 1.$
$ \Rightarrow T = a + 5b + {\log _{2018}}a = 6.$
$ \Rightarrow T = a + 5b + {\log _{2018}}a = 6.$
Chọn đáp án B.
Ví dụ 22: Cho hình bằng $D$ số lượng giới hạn bởi vì đàng cong $y = {e^x} + {e^{ – x}}$, trục hoành và những đường thẳng liền mạch $x=0$, $x=1.$ Khối tròn trặn xoay tạo ra trở nên khi xoay $D$ xung quanh trục hoành hoàn toàn có thể tích bởi vì $\pi \left( {\frac{{{e^2}}}{a} + \frac{{{e^{ – 2}}}}{b} + c} \right)$ với $a$, $b$, $c$ là những số nguyên vẹn.
Tính $T=a+b+2c.$
A. $T=-2.$
B. $T=0.$
C. $T=2.$
D. $T = 4.$
Lời giải:
$V = \pi \int_0^1 {{{\left( {{e^x} + {e^{ – x}}} \right)}^2}} dx$ $ = \pi \int_0^1 {\left( {{e^{2x}} + 2 + {e^{ – 2x}}} \right)dx} .$
$ = \left. {\pi \left( {\frac{{{e^{2x}}}}{2} + 2x – \frac{{{e^{ – 2x}}}}{2}} \right)} \right|_0^1$ $ = \pi \left( {\frac{{{e^2}}}{2} + 2 – \frac{{{e^{ – 2}}}}{2}} \right).$
$ \Rightarrow a = 2$, $b = – 2$, $c = 2$ $ \Rightarrow T = a + b + 2c = 4.$
Chọn đáp án D.
Ví dụ 23: Cho hình bằng $D$ số lượng giới hạn bởi vì đàng cong $y = \sqrt {{e^{2x}} – {e^x}} $, trục hoành và đường thẳng liền mạch $x=1.$ Khối tròn trặn xoay tạo ra trở nên khi xoay $D$ xung quanh trục hoành hoàn toàn có thể tích bởi vì $\pi \left( {\frac{{{e^2}}}{a} – e + \frac{1}{b}} \right)$ với $a$, $b$ là những số nguyên vẹn. Điểm $M(a;b)$ nằm trong thiết bị thị hàm số này sau đây?
A. $y = 5x + 1.$
B. $y = {x^2}.$
C. $y = {x^3} – 6.$
D. $y = {x^4} – 2.$
Lời giải:
Hoành chừng gửi gắm điểm:
$\sqrt {{e^{2x}} – {e^x}} = 0$ $ \Leftrightarrow x = 0.$
Thể tích: $V = \pi \int_0^1 {\left( {{e^{2x}} – {e^x}} \right)dx} $ $ = \left. {\pi \left( {\frac{1}{2}{e^{2x}} – {e^x}} \right)} \right|_0^1$ $ = \pi \left( {\frac{{{e^2}}}{2} – e + \frac{1}{2}} \right).$
$ \Rightarrow a = 2$, $b = 2$ $ \Rightarrow M(2;2)$ nằm trong thiết bị thị hàm số $y = {x^3} – 6.$
Chọn đáp án C.
Ví dụ 24: Cho hình bằng $D$ số lượng giới hạn bởi vì đàng cong $y = \sqrt {(1 – x){e^x}} $, trục hoành và trục tung. Khối tròn trặn xoay tạo ra trở nên khi xoay $D$ xung quanh trục hoành hoàn toàn có thể tích bởi vì $\pi (ae + b)$ với $a$, $b$ là những số nguyên vẹn. Điểm $I(a;b)$ là đỉnh của parabol này sau đây?
A. $y = {x^2} – 3.$
B. $y = {x^2} – 2x + 1.$
C. $y = {x^2} + 2x – 5.$
D. $y = {x^2} – 2x – 1.$
Lời giải:
Hoành chừng gửi gắm điểm: $\sqrt {(1 – x){e^x}} = 0$ $ \Leftrightarrow x = 1.$
Thể tích: $V = \pi \int_0^1 {(1 – x){e^x}dx} .$

$V = \left. {\pi \left[ {(1 – x){e^x} + {e^x}} \right]} \right|_0^1$ $ = \pi (e – 2)$ $ \Rightarrow a = 1$, $b = – 2.$
$ \Rightarrow I(1; – 2)$ là đỉnh của parabol $y = {x^2} – 2x – 1.$
Chọn đáp án D.
Ví dụ 25: Cho hình bằng $D$ số lượng giới hạn bởi vì đàng cong $y = (x – 2){e^x}$, trục hoành và trục tung. Khối tròn trặn xoay tạo ra trở nên khi xoay $D$ xung quanh trục hoành hoàn toàn có thể tích bởi vì $\pi \left( {\frac{{{e^4}}}{a} + \frac{b}{4}} \right)$ với $a$, $b$ là những số nguyên vẹn. Điểm $I(a;b)$ là tâm đối xứng của thiết bị thị hàm số này sau đây?
A. $y = \frac{{10x + 2016}}{{x – 4}}.$
B. $y = \frac{{11x + 2017}}{{2 – x}}.$
C. $y = \frac{{12x + 2018}}{{4 – x}}.$
D. $y = \frac{{13x + 2019}}{{4 – x}}.$
Lời giải:
Hoành chừng gửi gắm điểm: $(x – 2){e^x} = 0$ $ \Leftrightarrow x = 2.$
Thể tích: $V = \pi \int_0^2 {{{(x – 2)}^2}} {e^{2x}}dx.$
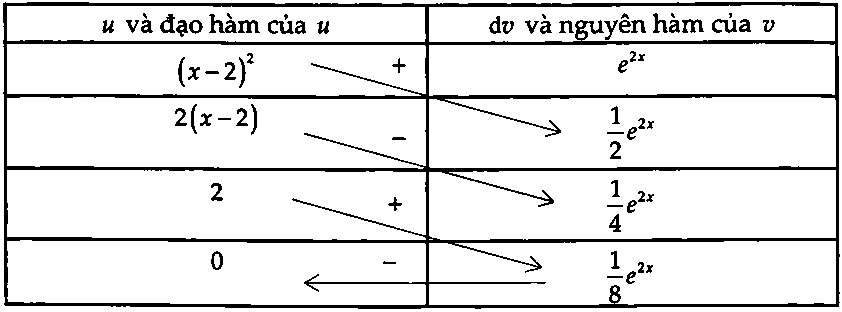
$V = \left. {\pi \left[ {\frac{{{{(x – 2)}^2}{e^{2x}}}}{2} – \frac{{(x – 2){e^{2x}}}}{2} + \frac{{{e^{2x}}}}{4}} \right]} \right|_0^2$ $ = \pi \left( {\frac{{{e^4}}}{4} – \frac{{13}}{4}} \right)$ $ \Rightarrow a = 4$, $b = – 13.$
$ \Rightarrow I(4; – 13)$ là tâm đối xứng của thiết bị thị hàm số $y = \frac{{13x + 2019}}{{4 – x}}.$
Chọn đáp án D.
Ví dụ 26: Cho hình bằng $D$ số lượng giới hạn bởi vì đàng cong $y = \sqrt {\frac{{\ln x}}{x}} $, trục hoành và những đường thẳng liền mạch $x = 1$, $x = {e^2}.$ Khối tròn trặn xoay tạo ra trở nên khi xoay $D$ xung quanh trục hoành hoàn toàn có thể tích bằng:
A. $1.$
B. $2.$
C. $3.$
D. $4.$
Lời giải:
$V = \pi \int_1^{{e^2}} {\frac{{\ln x}}{x}dx} $ $ = \pi \int_1^{{e^2}} {\ln xd(\ln x)} $ $ = \left. {\frac{{{{\ln }^2}x}}{2}} \right|_1^{{e^2}} = 2.$
Chọn đáp án B.
Ví dụ 27: Cho hình bằng $D$ số lượng giới hạn bởi vì đàng cong $y = \sqrt {(2x – 2)\ln x} $, trục hoành và đường thẳng liền mạch $x=2.$ Khối tròn trặn xoay tạo ra trở nên khi xoay $D$ xung quanh trục hoành hoàn toàn có thể tích bởi vì $\frac{a}{b}\pi $ với $a$ là số nguyên vẹn dương, $\frac{a}{b}$ là phân số tối giản. Tính $T = \ln {a^{2018}} + b.$
A. $2.$
B. $3.$
C. $2020.$
D. $2021.$
Lời giải:
Hoành chừng gửi gắm điểm: $\sqrt {(2x – 2)\ln x} = 0$ $ \Leftrightarrow x = 1.$
Thể tích: $V = \pi \int_1^2 {(2x – 2)} \ln xdx.$
Đặt $\left\{ {\begin{array}{*{20}{l}}
{u = \ln x}\\
{dv = (2x – 2)dx}
\end{array}} \right.$ $ \Rightarrow \left\{ {\begin{array}{*{20}{l}}
{du = \frac{1}{x}dx}\\
{v = {x^2} – 2x}
\end{array}} \right..$
$V = \pi \left[ {\left. {\left( {{x^2} – 2x} \right)\ln x} \right|_1^2 – \int_1^2 {(x – 2)dx} } \right]$ $ = \pi \left[ {\left. {\left( {{x^2} – 2x} \right)\ln x} \right|_1^2 – \left. {\left( {\frac{{{x^2}}}{2} – 2x} \right)} \right|_1^2} \right]$ $ = \frac{\pi }{2}.$
$ \Rightarrow a = 1$, $b = 2$ $ \Rightarrow T = \ln {a^{2018}} + b = 2.$
Chọn đáp án A.
III. LUYỆN TẬP
1. ĐỀ BÀI
Câu 1: Cho thể tích khối tròn xoay tạo ra trở nên khi xoay hình bằng số lượng giới hạn bởi vì những đàng $y = 3x – {x^2}$, $y = 0$ xung quanh trục $Ox$ bởi vì $\frac{a}{b}\pi $ với $a$, $b$ là những số nguyên vẹn dương và $\frac{a}{b}$ là phân số tối giản. Tính $T= a+2b.$
A. $T = 172.$
B. $T=101.$
C. $T=20.$
D. $T=13.$
Câu 2: Cho thể tích khối tròn xoay tạo ra trở nên khi xoay hình bằng số lượng giới hạn bởi vì những đàng $y = 2x – {x^2}$, $y = 0$ xung quanh trục $Ox$ bởi vì $\frac{a}{b}\pi $ với $a$, $b$ là những số nguyên vẹn dương và $\frac{a}{b}$ là phân số tối giản. Giá trị $2a+b$ nằm trong khoảng chừng này sau đây?
A. $(10;12).$
B. $(12;14).$
C. $(44;47).$
D. $(46;48).$
Câu 3: Cho thể tích khối tròn xoay tạo ra trở nên khi xoay hình bằng số lượng giới hạn bởi vì những đàng $y = \sin x$, $y = 0$, $x = 0$, $x = \pi $ xung quanh trục $Ox$ bởi vì $\frac{a}{b}{\pi ^2}$ với $a$, $b$ là những số nguyên vẹn dương và $\frac{a}{b}$ là phân số tối giản. Khẳng quyết định này sau đấy là đúng?
A. $a>b.$
B. $a<b.$
C. $a=b+3.$
D. $b=a+2.$
Câu 4: Cho thể tích khối tròn xoay tạo ra trở nên khi xoay hình bằng số lượng giới hạn bởi vì những đàng $y = \sqrt {\frac{x}{{4 – {x^2}}}} $, $y = 0$, $x = 1$ xung quanh trục $Ox$ bởi vì $\frac{\pi }{a}\ln \frac{b}{c}$ với $b$, $c$ là những số nguyên vẹn dương và $\frac{b}{c}$ là phân số tối giản. Tính $T = a+b-c.$
A. $T=1.$
B. $T=3.$
C. $T=4.$
D. $T=5.$
Câu 5: Cho thể tích khối tròn xoay tạo ra trở nên khi xoay hình bằng số lượng giới hạn bởi vì những đàng $y = \sqrt {{e^x}} $, $y = 0$, $x = 0$, $x = 1$ xung quanh trục $Ox$ bởi vì $\pi (ae + b)$ với $a$, $b$ là những số nguyên vẹn. Tính $T=5a+b.$
A. $T=-4.$
B. $T=-2.$
C. $T=2.$
D. $T=4.$
Câu 6: Cho thể tích khối tròn xoay tạo ra trở nên khi xoay hình bằng số lượng giới hạn bởi vì những đàng $y = \sqrt {{{\sin }^4}x + {{\cos }^4}x} $, $y = 0$, $x = \frac{\pi }{2}$, $x = \pi $ xung quanh trục $Ox$ bởi vì $\frac{a}{b}{\pi ^2}$ với $a$, $b$ là những số nguyên vẹn dương và $\frac{a}{b}$ là phân số tối giản. Tính chừng lâu năm đoạn trực tiếp $OA$ với $A(a;b).$
A. $OA = \sqrt {71} .$
B. $OA = \sqrt {72} .$
C. $OA = \sqrt {73} .$
D. $OA = \sqrt {74} .$
Câu 7: Cho thể tích khối tròn xoay tạo ra trở nên khi xoay hình bằng số lượng giới hạn bởi vì những đàng $y = \sqrt {x\sin x} $, $y = 0$, $x = 0$, $x = \pi $ xung quanh trục $Ox$ bởi vì $a{\pi ^2}.$ Tính khoảng cách $h$ kể từ điểm $A(1;a)$ cho tới đường thẳng liền mạch $\Delta :3x + 4y – 1 = 0.$
A. ${h = \frac{6}{5}.}$
B. ${h = \frac{7}{5}.}$
C. ${h = \frac{8}{5}.}$
D. ${h = \frac{9}{5}}.$
Câu 8: Cho thể tích khối tròn xoay tạo ra trở nên khi xoay hình bằng số lượng giới hạn bởi vì những đàng $y = \sqrt {\frac{{1 – x}}{x}} $ $(0 < x \le 1)$, $y = 0$, $x = \frac{1}{2}$ xung quanh trục $Ox$ bởi vì $V = \pi \left( {\ln 2 + \frac{a}{b}} \right)$ với $b$ là số nguyên vẹn dương và $\frac{a}{b}$ là phân số tối giản. Tính $T=2a+b.$
A. $T=0.$
B. $T=3.$
C. $T=5.$
D. $T=7.$
Câu 9: Cho thể tích khối tròn xoay tạo ra trở nên khi xoay hình bằng số lượng giới hạn bởi vì những đàng $y = x{e^x}$, $y = 0$, $x = 0$, $x = 2$ xung quanh trục $Ox$ bởi vì $\frac{\pi }{4}\left( {a{e^4} + b} \right).$ Tính $T= a + 2b.$
A. $T=1.$
B. $T =3.$
C. $T = 5.$
D. $T=9.$
Câu 10: Cho thể tích khối tròn xoay tạo ra trở nên khi xoay hình bằng số lượng giới hạn bởi vì những đàng $y = \sqrt {3 – \cos x} $, $y = 0$, $x = 0$, $x = \frac{\pi }{6}$ xung quanh trục $Ox$ bởi vì $\frac{{\pi (\pi – 1)}}{a}.$ Tính $T = {\log _2}a.$
A. $T=0.$
B. $T=1.$
C. $T=2.$
D. $T =3.$
2. BẢNG ĐÁP ÁN
| Câu | 1 | 2 | 3 | 4 | 5 |
| Đáp án | B | D | B | B | D |
| Câu | 6 | 7 | 8 | 9 | 10 |
| Đáp án | C | A | A | B | B |










Bình luận